Square Root Of Negative 7
saludintensiva
Sep 20, 2025 · 5 min read
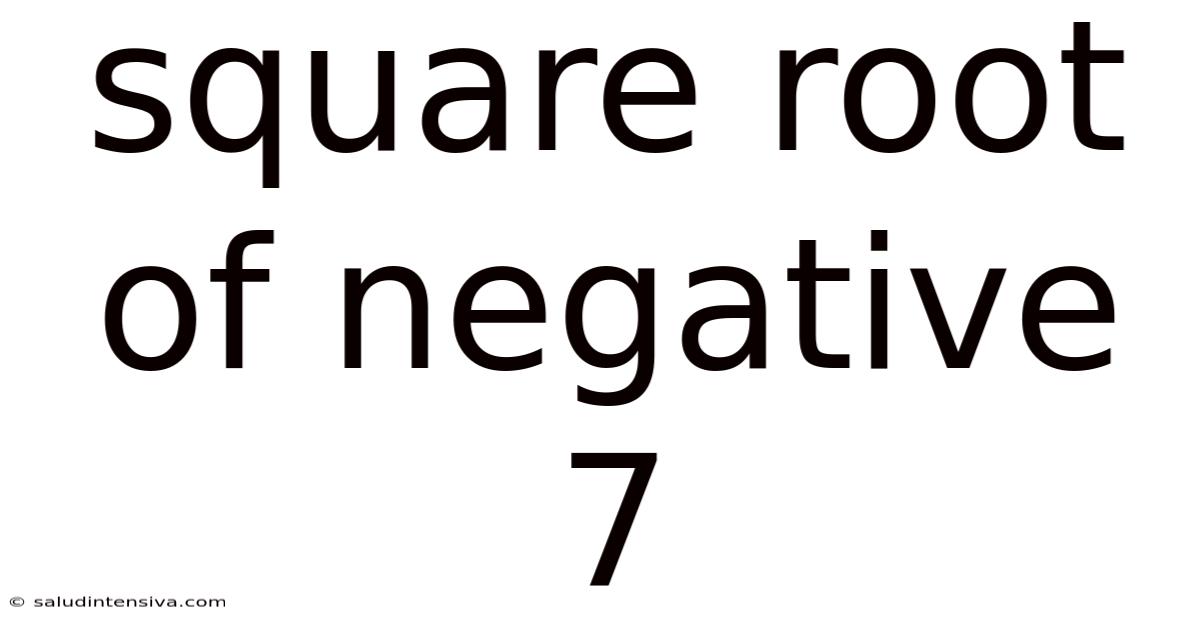
Table of Contents
Delving into the Depths: Understanding the Square Root of Negative 7
The concept of the square root of negative seven, √-7, might seem initially perplexing. After all, we learn early on that the square of any real number is always positive. How can a number multiplied by itself result in a negative value? This question leads us down a fascinating path into the world of imaginary numbers and complex numbers, a realm that expands our understanding of mathematics beyond the familiar real number line. This article will explore the square root of -7, explaining its nature, its properties, and its significance within the broader mathematical landscape.
Understanding the Basics: Real and Imaginary Numbers
Before we tackle √-7, let's establish a foundational understanding. The real numbers comprise all the numbers we typically encounter: positive and negative whole numbers (integers), fractions (rational numbers), and numbers like π (irrational numbers) that cannot be expressed as a simple fraction. These numbers can be represented on a number line, extending infinitely in both positive and negative directions.
However, the equation x² = -1 has no solution within the set of real numbers. To address this, mathematicians introduced the imaginary unit, denoted by i, defined as:
i² = -1
This seemingly simple definition opens up a whole new world of numbers. The square root of -1 is i, and we can express the square root of any negative number using i.
Defining √-7: Introducing Complex Numbers
Now, let's return to our original question: what is √-7? Using the properties of square roots and the imaginary unit, we can express it as follows:
√-7 = √(-1 * 7) = √-1 * √7 = i√7
Therefore, the square root of -7 is i√7. This is a complex number, which is a number that combines a real part and an imaginary part. In this case:
- Real part: 0
- Imaginary part: √7
A general complex number is represented as a + bi, where a is the real part and b is the imaginary part. So, √-7 can be written as 0 + √7i.
Visualizing Complex Numbers: The Complex Plane
While real numbers can be visualized on a single number line, complex numbers require a two-dimensional representation. The complex plane, also known as the Argand plane, uses a horizontal axis for the real part and a vertical axis for the imaginary part. Each complex number is represented by a point on this plane. The complex number √-7 would be located on the positive imaginary axis, at a distance of √7 units from the origin.
Operations with √-7 and Other Complex Numbers
We can perform arithmetic operations (addition, subtraction, multiplication, and division) on complex numbers, including √-7. Here are some examples:
- Addition: (2 + 3i) + (0 + √7i) = 2 + (3 + √7)i
- Subtraction: (2 + 3i) - (0 + √7i) = 2 + (3 - √7)i
- Multiplication: (2 + 3i)(√7i) = 2√7i + 3√7i² = -3√7 + 2√7i
- Division: Dividing complex numbers involves a process similar to rationalizing the denominator, using the complex conjugate.
The Significance of √-7 and Complex Numbers
The seemingly abstract concept of complex numbers has profound implications across various branches of science and engineering. Here are some key applications:
-
Electrical Engineering: Complex numbers are essential for analyzing alternating current (AC) circuits, where impedance and phase shifts are crucial considerations. The imaginary part of a complex number often represents the reactive component of impedance (inductance and capacitance).
-
Quantum Mechanics: Complex numbers are fundamental to the mathematical formulation of quantum mechanics, describing the wave function of particles and their probabilities.
-
Signal Processing: Complex numbers are used extensively in signal processing for representing and manipulating signals in the frequency domain using techniques like the Fourier transform.
-
Fluid Dynamics: Complex analysis is used to model fluid flow and solve problems related to aerodynamics and hydrodynamics.
-
Fractals and Chaos Theory: Iterative processes involving complex numbers lead to the generation of stunning fractal patterns, revealing unexpected connections between seemingly chaotic systems.
Solving Equations Involving √-7
Understanding complex numbers enables us to solve equations that would be unsolvable within the realm of real numbers. Consider a simple quadratic equation:
x² + 7 = 0
Solving for x, we get:
x² = -7
x = ±√-7 = ±√7i
This demonstrates that even simple equations can have complex number solutions.
Frequently Asked Questions (FAQ)
Q1: Is √-7 a real number?
No, √-7 is not a real number. It's an imaginary number, specifically a complex number with a real part of 0 and an imaginary part of √7.
Q2: Can we simplify √-7 further?
The expression √-7 is already in a simplified form. We can express it as i√7, but we cannot simplify √7 further without resorting to approximations.
Q3: What is the conjugate of √-7?
The conjugate of a complex number a + bi is a - bi. Since √-7 = 0 + i√7, its conjugate is 0 - i√7 or simply -i√7.
Q4: What is the magnitude or modulus of √-7?
The magnitude (or modulus) of a complex number a + bi is given by √(a² + b²). For √-7 (0 + i√7), the magnitude is √(0² + (√7)²) = √7.
Q5: How are complex numbers used in everyday life (indirectly)?
While we don't explicitly work with complex numbers in everyday tasks, they are integral to many technologies we use, such as smartphones, computers, and GPS systems, which rely on algorithms and processes that utilize complex number calculations.
Conclusion: Expanding Mathematical Horizons
The exploration of the square root of negative seven, while seemingly esoteric, unveils a deeper understanding of the mathematical universe. The introduction of the imaginary unit i and the resulting complex numbers dramatically expand our mathematical toolkit, allowing us to solve problems and model phenomena that were previously inaccessible. While the concept might seem abstract at first, the power and practicality of complex numbers are undeniable, extending far beyond the realm of theoretical mathematics and deeply impacting various fields of science and engineering. Understanding √-7 is not just about grasping a single mathematical concept; it is about appreciating the evolution and richness of mathematics and its capacity to reveal the hidden structures of our world.
Latest Posts
Latest Posts
-
What Is 1 5 Of 10
Sep 20, 2025
-
What Are Factors Of 76
Sep 20, 2025
-
What Times What Equals 42
Sep 20, 2025
-
Ml To Gallons Conversion Calculator
Sep 20, 2025
-
Nepali Date Converter To English
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of Negative 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.