Square Root Of X 3
saludintensiva
Sep 15, 2025 · 6 min read
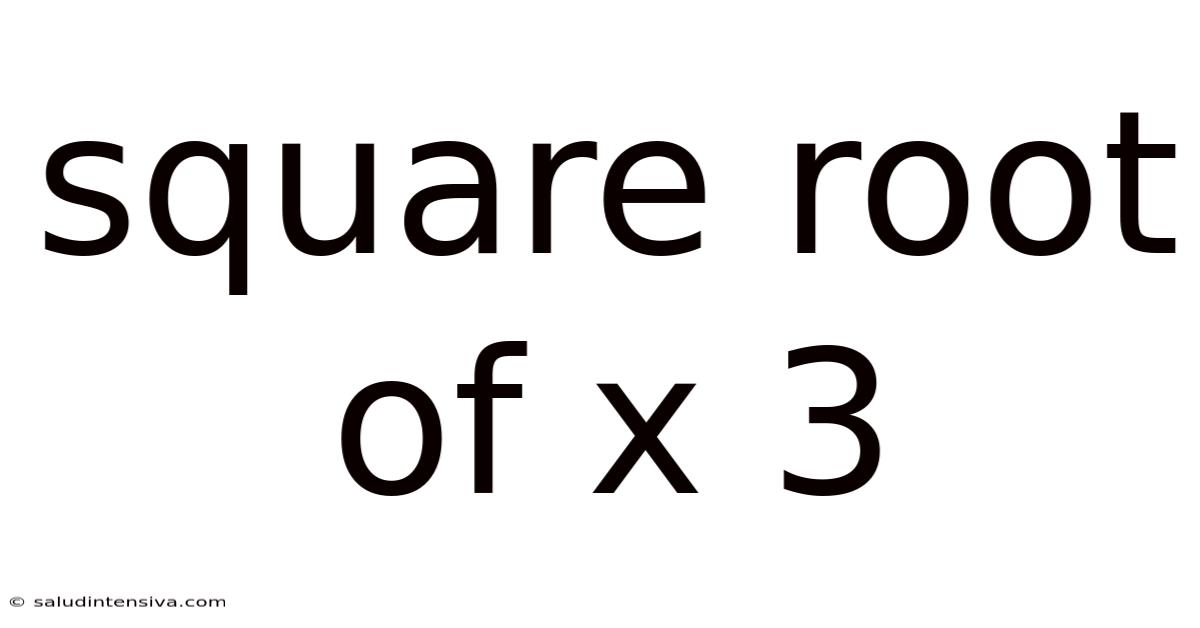
Table of Contents
Unveiling the Mysteries of the Cube Root of x: A Comprehensive Guide
Understanding the cube root of a number, often represented as ³√x or x^(1/3), is a fundamental concept in mathematics with applications spanning various fields, from basic algebra to advanced calculus and even computer science. This comprehensive guide will delve into the intricacies of cube roots, exploring their definition, calculation methods, properties, and real-world applications. We'll break down the complexities into digestible chunks, ensuring that even those with limited mathematical backgrounds can grasp this essential concept.
What is the Cube Root of x?
The cube root of a number x is the number that, when multiplied by itself three times, equals x. In simpler terms, if y³ = x, then y is the cube root of x (³√x = y). For example, the cube root of 8 is 2 because 2 * 2 * 2 = 8. Unlike square roots, which can have both positive and negative solutions (except for zero), the cube root of a positive number is always positive, and the cube root of a negative number is always negative. The cube root of zero is, of course, zero. This seemingly simple definition opens the door to a surprisingly rich mathematical landscape.
Methods for Calculating the Cube Root of x
Calculating cube roots can be approached in several ways, depending on the complexity of the number and the tools available.
1. Prime Factorization Method:
This method is best suited for perfect cubes – numbers that have exact cube roots. It involves expressing the number as a product of its prime factors and then grouping them into sets of three.
-
Example: Find the cube root of 216.
- Prime factorize 216: 216 = 2 x 2 x 2 x 3 x 3 x 3
- Group the factors into sets of three: (2 x 2 x 2) x (3 x 3 x 3)
- The cube root is the product of one factor from each group: 2 x 3 = 6. Therefore, ³√216 = 6.
This method is efficient for perfect cubes, but it's less practical for non-perfect cubes.
2. Estimation and Iteration Methods:
For non-perfect cubes, estimation and iterative methods are necessary. One common approach is the Newton-Raphson method, a powerful numerical technique for finding approximations of roots. While the mathematical details of the Newton-Raphson method are beyond the scope of this introductory guide, its core idea is to refine an initial guess through successive iterations, getting closer to the actual cube root with each step.
- Example (Conceptual): Let's say we want to find the cube root of 10. We start with an initial guess, say 2 (because 2³ = 8, which is close to 10). The Newton-Raphson method would then use a formula to refine this guess, generating a closer approximation, say 2.15. This process is repeated until the desired level of accuracy is achieved. Calculators and computer programs use similar iterative methods to compute cube roots.
3. Using a Calculator or Computer Software:
The most straightforward method for calculating cube roots, especially for complex numbers, is using a calculator or mathematical software. Most scientific calculators have a dedicated cube root function (often denoted as ³√ or x^(1/3)). Similarly, software like MATLAB, Python (with libraries like NumPy), and others provide functions for efficiently computing cube roots.
Properties of Cube Roots
Cube roots possess several important mathematical properties:
- Product Rule: The cube root of a product is the product of the cube roots: ³√(ab) = ³√a * ³√b.
- Quotient Rule: The cube root of a quotient is the quotient of the cube roots: ³√(a/b) = ³√a / ³√b (provided b ≠ 0).
- Power Rule: The cube root of a number raised to a power is equal to the number raised to the power divided by 3: ³√(aⁿ) = a^(n/3).
- Inverse Relationship with Cubing: Cubing a number and taking its cube root are inverse operations. This means (³√x)³ = x.
Cube Roots in the Real World
The concept of the cube root is far from being a purely theoretical exercise; it finds practical application in various real-world scenarios:
- Volume Calculations: The cube root is crucial in determining the side length of a cube given its volume. If you know the volume (V) of a cube, the length of its side (s) is simply ³√V. This has applications in numerous fields, from engineering and architecture to packaging and manufacturing.
- Physics and Engineering: Cube roots appear in various physics and engineering formulas, particularly those related to volume, density, and other three-dimensional quantities. For instance, calculations involving fluid dynamics or structural mechanics might utilize cube roots.
- Data Analysis and Statistics: In statistical analysis, cube roots can be used for data transformations to address skewed distributions, making data more amenable to certain statistical techniques.
- Finance and Economics: While less frequent than square roots, cube roots might occasionally appear in some financial models, especially those involving complex calculations of growth or decay over time.
- Computer Graphics and Game Development: Cube roots and related mathematical functions are fundamental to computer graphics and game development, particularly in rendering three-dimensional models and simulations.
Complex Cube Roots
While our discussion so far has primarily focused on real numbers, cube roots can also be extended to the realm of complex numbers. A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit (√-1). Every non-zero complex number has three distinct cube roots, which are equally spaced around a circle in the complex plane. Understanding complex cube roots requires a deeper understanding of complex number arithmetic and polar coordinates.
Frequently Asked Questions (FAQs)
-
Q: What is the cube root of a negative number?
- A: The cube root of a negative number is a negative number. For example, ³√(-8) = -2, because (-2)³ = -8.
-
Q: Can a cube root be negative?
- A: Yes, the cube root of a negative number is negative.
-
Q: How do I calculate the cube root of a very large number?
- A: For very large numbers, using a calculator or computer software is the most efficient approach. Iterative methods, such as the Newton-Raphson method, are also effective, albeit more complex to implement manually.
-
Q: What is the cube root of 1?
- A: The cube root of 1 is 1 (1³ = 1).
-
Q: Are there any shortcuts for calculating cube roots mentally?
- A: For perfect cubes, recognizing patterns and prime factorizations can help. However, for most numbers, mental calculation of cube roots is impractical without considerable practice and memorization.
Conclusion
The cube root of x, a seemingly simple concept, opens doors to a wide range of mathematical applications and real-world problems. Understanding its definition, calculation methods, and properties is crucial for anyone pursuing studies in mathematics, science, engineering, or computer science. While calculators and computers readily provide numerical solutions, grasping the underlying principles offers a deeper appreciation of this fundamental mathematical operation and its role in shaping our understanding of the world around us. By mastering the cube root, we equip ourselves with a powerful tool for tackling complex problems across multiple disciplines. From calculating volumes to analyzing data, the applications are vast and constantly expanding, showcasing the enduring significance of this key mathematical function.
Latest Posts
Latest Posts
-
75 100 As A Decimal
Sep 15, 2025
-
Lcm Of 13 And 9
Sep 15, 2025
-
7 1 2 As A Decimal
Sep 15, 2025
-
Gcf Of 12 And 32
Sep 15, 2025
-
Convert 64 Into A Fraction
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.