What Does 1 4 Equal
saludintensiva
Sep 10, 2025 · 6 min read
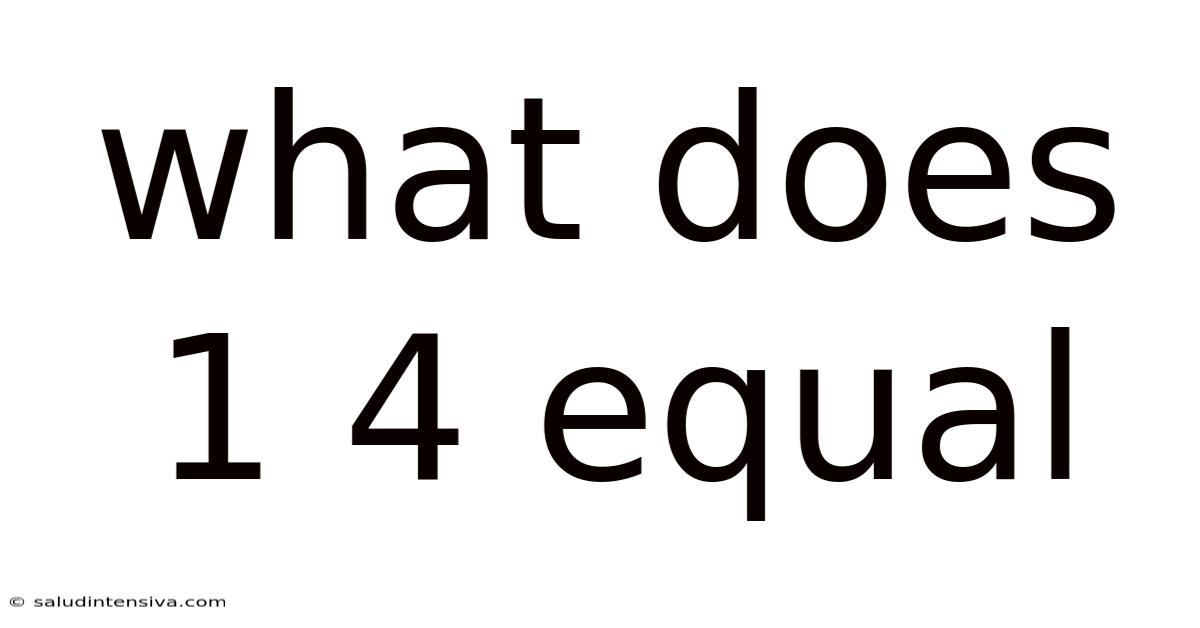
Table of Contents
What Does 1/4 Equal? A Deep Dive into Fractions and Their Applications
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article will explore the meaning of 1/4, delve into its various representations, and show how it applies across different contexts. We'll unpack the concept thoroughly, addressing common questions and misconceptions along the way. By the end, you'll have a solid grasp of what 1/4 equals and its significance in the broader mathematical landscape.
Understanding Fractions: The Basics
Before we dive into the specifics of 1/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 3/8, the numerator (3) signifies that we have three parts, and the denominator (8) indicates that the whole has been divided into eight equal parts.
What Does 1/4 Equal? The Simple Answer
1/4, also known as one-quarter or a quarter, simply means one out of four equal parts. If you divide a whole into four identical pieces, then 1/4 represents one of those pieces.
Visualizing 1/4
Visual representations can make understanding fractions much easier. Imagine a pizza cut into four equal slices. One slice represents 1/4 of the whole pizza. Similarly, consider a chocolate bar broken into four equal squares. One square is 1/4 of the bar. These visual aids help solidify the concept of 1/4 as a portion of a whole.
Different Representations of 1/4
1/4 can be represented in several ways, all conveying the same value:
- Decimal: 1/4 is equal to 0.25. This is obtained by dividing the numerator (1) by the denominator (4).
- Percentage: 1/4 is equivalent to 25%. This is because percentages represent fractions out of 100. To convert 1/4 to a percentage, we multiply it by 100: (1/4) * 100 = 25%.
- Ratio: 1/4 can be expressed as a ratio of 1:4. This signifies a proportion where one part is compared to a total of four parts.
Practical Applications of 1/4
The concept of 1/4 is used extensively in everyday life and various fields:
- Cooking and Baking: Recipes often call for 1/4 cup or 1/4 teaspoon of an ingredient. Understanding fractions is essential for accurate measurements and successful cooking.
- Measurements: Measuring tools like rulers and tape measures often have markings indicating 1/4 of an inch or centimeter.
- Money: A quarter is 1/4 of a dollar.
- Time: 15 minutes is 1/4 of an hour (60 minutes).
- Geometry: 1/4 of a circle represents a 90-degree angle (a right angle).
- Data Analysis: Fractions, including 1/4, are fundamental to understanding proportions and percentages in data analysis and statistics.
Equivalent Fractions to 1/4
An important concept in working with fractions is understanding equivalent fractions. These are fractions that represent the same value, even though they look different. You can create equivalent fractions by multiplying or dividing both the numerator and denominator by the same number (except zero).
For example:
- 2/8 is equivalent to 1/4 (multiply both numerator and denominator of 1/4 by 2)
- 3/12 is equivalent to 1/4 (multiply both numerator and denominator of 1/4 by 3)
- 4/16 is equivalent to 1/4 (multiply both numerator and denominator of 1/4 by 4)
Understanding equivalent fractions allows you to simplify fractions and compare them more easily.
Adding and Subtracting Fractions Involving 1/4
To add or subtract fractions, they must have a common denominator. If one of the fractions is 1/4, and the other fraction has a different denominator, you'll need to find the least common multiple (LCM) of the denominators. Then, you convert each fraction to an equivalent fraction with the common denominator before performing the addition or subtraction.
Example:
Add 1/4 and 1/2.
- The LCM of 4 and 2 is 4.
- Convert 1/2 to an equivalent fraction with a denominator of 4: 1/2 * 2/2 = 2/4.
- Now add the fractions: 1/4 + 2/4 = 3/4
Multiplying and Dividing Fractions Involving 1/4
Multiplying fractions is straightforward: multiply the numerators together and multiply the denominators together. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
Example:
- Multiply 1/4 by 2/3: (1/4) * (2/3) = 2/12 = 1/6 (simplified)
- Divide 1/4 by 1/2: (1/4) / (1/2) = (1/4) * (2/1) = 2/4 = 1/2 (simplified)
Working with Mixed Numbers and 1/4
A mixed number combines a whole number and a fraction. For example, 2 1/4 means two whole units plus one-quarter of a unit.
To add, subtract, multiply, or divide mixed numbers involving 1/4, it's often easier to convert the mixed number into an improper fraction first. An improper fraction has a numerator larger than or equal to its denominator.
Example: Convert 2 1/4 to an improper fraction:
- Multiply the whole number by the denominator: 2 * 4 = 8
- Add the numerator: 8 + 1 = 9
- Keep the same denominator: 9/4
Advanced Applications: Calculus and Beyond
While this article focuses on the basic understanding of 1/4, it's important to note that the concept of fractions and their decimal equivalents forms the foundation of many advanced mathematical concepts. In calculus, for instance, understanding limits and derivatives often involves working with fractions and infinitesimals.
Frequently Asked Questions (FAQ)
Q: What is 1/4 as a decimal?
A: 1/4 is equal to 0.25.
Q: What is 1/4 as a percentage?
A: 1/4 is equal to 25%.
Q: How do I convert 1/4 to an equivalent fraction?
A: Multiply both the numerator and denominator by the same number (e.g., 2/8, 3/12, 4/16 are all equivalent to 1/4).
Q: Is there a simpler way to understand 1/4?
A: Think of dividing something into four equal parts. 1/4 represents one of those four parts.
Q: How can I use 1/4 in real-world situations?
A: It's used in cooking (measuring ingredients), money (a quarter), time (15 minutes), and many other areas.
Conclusion: Mastering 1/4 and Beyond
Understanding the concept of 1/4 is not merely about memorizing a fact; it's about grasping the fundamental principles of fractions, which are vital in numerous aspects of life and advanced mathematics. By visualizing 1/4, understanding its various representations, and exploring its applications, you've taken a significant step towards mastering fractions and developing a stronger foundation in mathematics. This knowledge will serve you well in various academic and practical pursuits. Remember to practice regularly, apply your knowledge to real-world scenarios, and don't hesitate to explore more complex fraction concepts to further enhance your understanding.
Latest Posts
Latest Posts
-
What Is Half Of 78
Sep 10, 2025
-
Lcm Of 4 And 30
Sep 10, 2025
-
5 Root 3 Whole Square
Sep 10, 2025
-
5 1 2 As A Decimal
Sep 10, 2025
-
11 2 As A Mixed Number
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Does 1 4 Equal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.