What Does 3 5 Equal
saludintensiva
Sep 14, 2025 · 6 min read
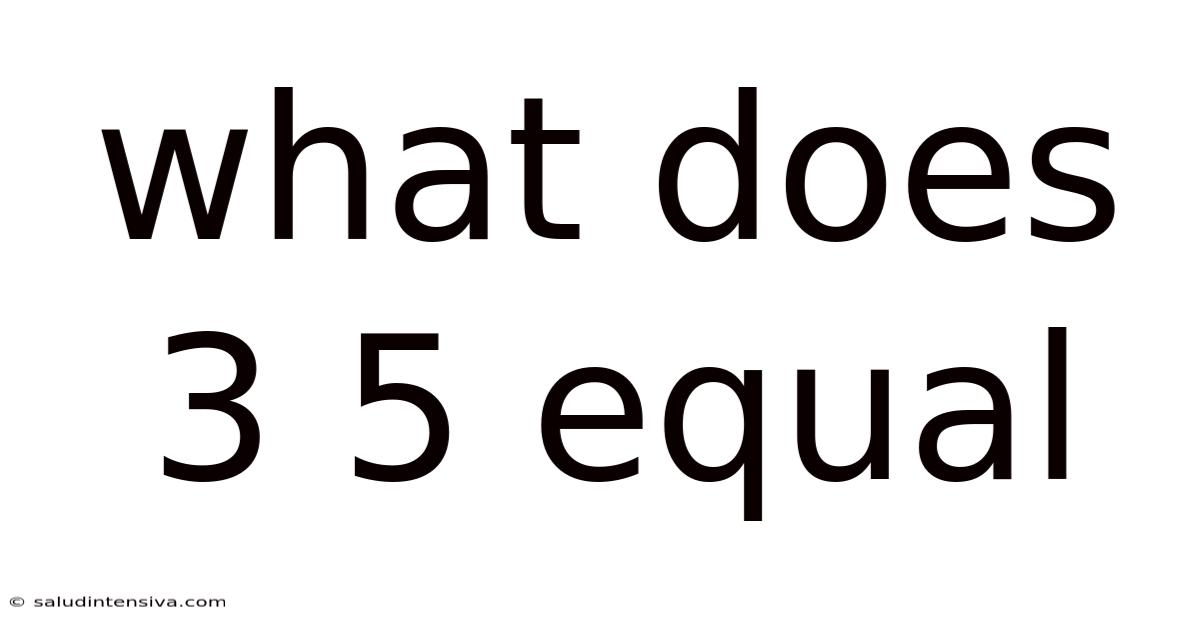
Table of Contents
What Does 3 x 5 Equal? A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple question: "What does 3 x 5 equal?" While the answer – 15 – is readily apparent to most, delving deeper reveals a wealth of mathematical concepts, practical applications, and even historical context surrounding this fundamental operation. Understanding multiplication, even at this basic level, is crucial for navigating various aspects of life, from everyday calculations to complex scientific endeavors.
Introduction to Multiplication: Beyond Simple Arithmetic
Multiplication, at its core, is repeated addition. 3 x 5 literally means adding the number 3 to itself five times: 3 + 3 + 3 + 3 + 3 = 15. However, multiplication is much more than just a shortcut for addition. It represents a fundamental concept in mathematics, forming the bedrock for numerous other operations and concepts, including division, algebra, calculus, and more. Understanding this foundational aspect is key to unlocking a deeper appreciation of the broader mathematical world. We will explore the concept of multiplication further, discussing its properties, applications, and relevance in various fields.
Understanding the Components: Multiplicand, Multiplier, and Product
Before delving into the intricacies, let's define the terms involved:
- Multiplicand: This is the number being multiplied (in our example, 3).
- Multiplier: This is the number indicating how many times the multiplicand is being added (in our example, 5).
- Product: This is the result of the multiplication (in our example, 15).
These seemingly simple definitions lay the groundwork for understanding more complex multiplicative operations.
Visualizing Multiplication: Arrays and Area Models
One effective way to visualize multiplication is through the use of arrays. An array is a rectangular arrangement of objects organized into rows and columns. For 3 x 5, you can imagine a rectangle with 3 rows and 5 columns. Counting the total number of objects in this array gives you the product, 15.
Another helpful visualization is the area model. Imagine a rectangle with a length of 5 units and a width of 3 units. The area of this rectangle (length x width) is 15 square units. This approach directly connects multiplication to geometry, illustrating its practical applications in calculating areas and volumes.
The Commutative Property: Order Doesn't Matter (Sometimes)
Multiplication possesses a crucial property called the commutative property. This means that the order of the numbers doesn't affect the product. 3 x 5 is the same as 5 x 3; both equal 15. This property simplifies calculations and allows for flexibility in problem-solving. However, it's important to note that this property doesn't apply to all mathematical operations, such as subtraction or division.
The Associative Property: Grouping Numbers for Easier Calculations
The associative property allows you to regroup numbers in a multiplication problem without changing the product. For example, if you have (2 x 3) x 5, you can calculate 2 x 3 first (which equals 6), then multiply by 5 (6 x 5 = 30). Alternatively, you could calculate 3 x 5 first (15), then multiply by 2 (2 x 15 = 30). The result remains the same. This property is invaluable for simplifying complex calculations.
The Distributive Property: Breaking Down Multiplication
The distributive property allows you to break down multiplication problems into smaller, more manageable parts. For example, if you need to calculate 3 x (5 + 2), you can distribute the 3 to both terms inside the parentheses: (3 x 5) + (3 x 2) = 15 + 6 = 21. This property is frequently used in algebra and other advanced mathematical fields.
Multiplication with Larger Numbers: Techniques and Strategies
While 3 x 5 is straightforward, multiplying larger numbers requires specific techniques. These include:
- Standard Algorithm: This involves multiplying each digit of one number by each digit of the other number, carrying over digits as needed. This method provides a systematic approach for multiplying numbers of any size.
- Lattice Multiplication: This visual method uses a grid to break down the multiplication into smaller, more manageable parts. It's particularly helpful for visualizing the process and understanding the underlying logic.
- Mental Math Techniques: With practice, you can develop mental math skills to quickly calculate products without relying on written methods. This involves using techniques like breaking down numbers, using known facts, and leveraging the commutative and associative properties.
Real-World Applications of Multiplication: From Shopping to Science
Multiplication isn't just an abstract mathematical concept; it has numerous practical applications in daily life and various professional fields:
- Shopping: Calculating the total cost of multiple items at the same price (e.g., 5 apples at $3 each).
- Cooking: Scaling recipes up or down (e.g., doubling a recipe that calls for 3 cups of flour).
- Construction: Calculating the area of a room or the volume of a container.
- Finance: Calculating interest, calculating total earnings based on hourly rates, or determining the total cost of investments.
- Science: Numerous scientific formulas involve multiplication, from calculating speed (distance x time) to determining the area of a circle (πr²).
Multiplication in Different Number Systems
While our example uses base-10 numbers (the decimal system), multiplication applies to other number systems as well, such as binary (base-2), used extensively in computer science. Understanding the principles of multiplication remains consistent across different numerical bases.
The History of Multiplication: Evolution of Techniques and Symbols
The history of multiplication is rich and spans centuries. Early civilizations developed various methods for multiplication, often involving different notations and techniques. The development of symbols and algorithms for multiplication reflects the evolution of mathematical understanding and the need for efficient calculation methods. From ancient Egyptian multiplication techniques to the development of the modern algorithms, the journey of multiplication showcases human ingenuity and the ongoing quest to refine mathematical tools.
Frequently Asked Questions (FAQ)
-
Q: What is the inverse operation of multiplication? A: Division. Division undoes multiplication. If 3 x 5 = 15, then 15 ÷ 5 = 3 and 15 ÷ 3 = 5.
-
Q: What happens when you multiply by zero? A: Any number multiplied by zero equals zero (e.g., 3 x 0 = 0). This is a fundamental property of multiplication.
-
Q: What happens when you multiply by one? A: Any number multiplied by one equals itself (e.g., 3 x 1 = 3). This is the identity property of multiplication.
-
Q: How do I multiply fractions? A: To multiply fractions, multiply the numerators (top numbers) together and multiply the denominators (bottom numbers) together. For example, (1/2) x (2/3) = (1 x 2) / (2 x 3) = 2/6 = 1/3.
-
Q: How do I multiply decimals? A: Multiply decimals as you would whole numbers, then count the total number of decimal places in both numbers. Place the decimal point in the product so that it has the same number of decimal places. For example, 3.2 x 2.5 = 8.00.
Conclusion: The Enduring Importance of Multiplication
The seemingly simple question "What does 3 x 5 equal?" opens a door to a vast and fascinating world of mathematics. Understanding multiplication, from its basic definition to its advanced applications, is essential for navigating everyday life and pursuing various academic and professional endeavors. The concepts explored – from the commutative and associative properties to the various techniques for calculating products – highlight the richness and depth of this fundamental mathematical operation. Its importance extends far beyond simple arithmetic, serving as a building block for more complex mathematical concepts and a crucial tool across numerous fields. Mastering multiplication is not just about getting the right answer; it's about understanding the underlying principles and appreciating its profound significance in the world around us.
Latest Posts
Latest Posts
-
Lcm Of 8 12 6
Sep 14, 2025
-
7 1 4 Improper Fraction
Sep 14, 2025
-
How Far Is 2 M
Sep 14, 2025
-
9 To The 6 Power
Sep 14, 2025
-
17 25 As A Percent
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Does 3 5 Equal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.