What Is 15 Of 30
saludintensiva
Sep 13, 2025 · 6 min read
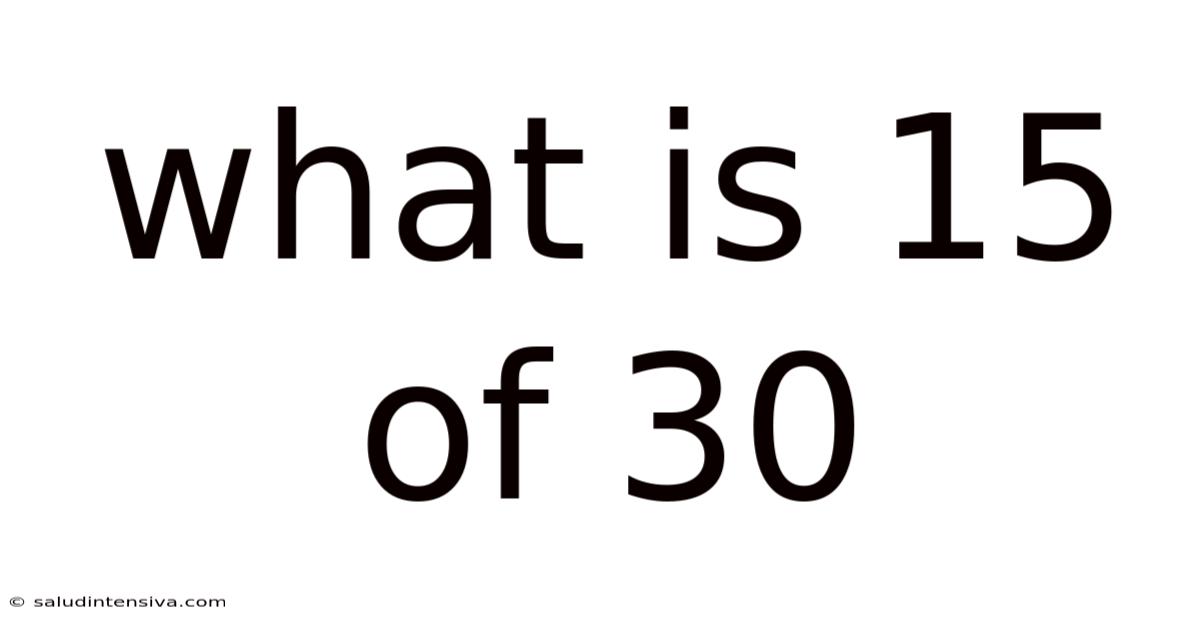
Table of Contents
What is 15 of 30? Understanding Fractions, Percentages, and Ratios
This seemingly simple question, "What is 15 of 30?", opens the door to a deeper understanding of fundamental mathematical concepts like fractions, percentages, and ratios. It's more than just a simple calculation; it's a gateway to grasping how these concepts relate to each other and how they're applied in everyday life. This article will explore various ways to solve this problem, delve into the underlying mathematical principles, and provide practical examples to solidify your understanding.
Understanding the Question: Fractions, Percentages, and Ratios
The question "What is 15 of 30?" can be interpreted in several ways, all revolving around the relationship between 15 and 30. It's essentially asking what proportion or fraction 15 represents of the total 30. We can express this relationship using different mathematical tools:
- Fraction: The most direct way to represent this is as a fraction: 15/30. This reads as "15 out of 30".
- Percentage: We can express the relationship as a percentage, indicating what percent 15 is of 30.
- Ratio: We can also express the relationship as a ratio, comparing 15 to 30.
Let's explore each method in detail.
Method 1: Solving as a Fraction – Simplifying Fractions
The simplest approach is to represent the relationship as a fraction: 15/30. This fraction can be simplified by finding the greatest common divisor (GCD) of both the numerator (15) and the denominator (30). The GCD of 15 and 30 is 15. Dividing both the numerator and the denominator by 15, we get:
15 ÷ 15 / 30 ÷ 15 = 1/2
Therefore, 15 is one-half of 30. This is the simplest and most fundamental representation of the relationship. Simplifying fractions is crucial not only for easier understanding but also for comparing fractions and performing further calculations. Understanding the concept of simplifying fractions is fundamental to many areas of mathematics and beyond. It lays the groundwork for more advanced topics like algebraic fractions and calculus.
Method 2: Solving as a Percentage – Converting Fractions to Percentages
To express the relationship as a percentage, we first represent it as a fraction (15/30), then convert the fraction to a decimal, and finally multiply by 100 to obtain the percentage.
-
Fraction to Decimal: Divide the numerator (15) by the denominator (30): 15 ÷ 30 = 0.5
-
Decimal to Percentage: Multiply the decimal by 100: 0.5 x 100 = 50%
Therefore, 15 is 50% of 30. This percentage representation is particularly useful for comparing proportions and making relative comparisons across different datasets. For example, if you scored 15 out of 30 on a test, you scored 50%, which is a common and easily understood way to represent your performance. The ability to convert fractions to percentages and vice-versa is a cornerstone of practical mathematics applicable in fields ranging from finance to data analysis.
Method 3: Solving as a Ratio – Understanding Proportions
A ratio expresses the relationship between two quantities. In this case, the ratio of 15 to 30 is written as 15:30. Like fractions, ratios can be simplified by dividing both numbers by their GCD (15):
15 ÷ 15 : 30 ÷ 15 = 1:2
This simplified ratio, 1:2, means that for every one unit of the first quantity, there are two units of the second quantity. Ratios are frequently used in various applications, such as scaling recipes, mixing ingredients, and comparing different measurements. Mastering ratios is essential for understanding concepts in geometry, chemistry, and other scientific disciplines. The understanding of ratios also extends to solving proportional problems, a crucial skill in various fields.
Practical Applications: Real-World Examples
The concepts of fractions, percentages, and ratios are interwoven in everyday life. Here are some practical examples illustrating their application:
- Shopping: If a shirt costs $30 and is on sale for $15, the discount is 15/30 or 50% off.
- Cooking: A recipe calls for 30 grams of flour and you only want to make half the recipe. You would use 15 grams (1/2 or 50%).
- Sports: If a basketball player makes 15 out of 30 shots, their shooting percentage is 50%.
- Finance: If you invest $30 and earn a profit of $15, your return on investment is 50%.
- Data Analysis: Analyzing survey data often involves calculating percentages and ratios to understand trends and make inferences.
These are just a few simple examples. The applications of these mathematical concepts are vast and extend to virtually every field. Understanding how to work with fractions, percentages, and ratios is fundamental to navigating and comprehending information presented numerically.
Further Exploration: Expanding Your Understanding
Understanding "What is 15 of 30?" is a stepping stone to more advanced mathematical concepts. Here are some areas to explore further:
- Proportions: Solving problems involving proportional relationships (e.g., if 15 is 50% of 30, what is 25% of 30?).
- Algebra: Applying algebraic equations to solve problems involving fractions, percentages, and ratios (e.g., solving for an unknown quantity in a proportion).
- Geometry: Using ratios and proportions to solve geometrical problems (e.g., similar triangles).
- Statistics: Using percentages and ratios to analyze data and draw conclusions.
Expanding your knowledge in these areas will build a strong foundation in mathematics and enhance your ability to solve complex problems.
Frequently Asked Questions (FAQ)
Q: What if the numbers weren't so easily divisible?
A: If the numbers were less easily divisible, you would still follow the same principles. Use prime factorization to find the GCD, simplifying the fraction to its lowest terms. Then, convert the fraction to a decimal and percentage as before. Calculators can assist in this process for larger or more complex numbers.
Q: Is there more than one way to express this relationship?
A: Yes, as demonstrated, the relationship between 15 and 30 can be expressed as a fraction (1/2), a percentage (50%), and a ratio (1:2). Each representation offers a unique perspective and is valuable in different contexts.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand and work with. It also makes it simpler to compare fractions and perform calculations involving fractions.
Q: How can I improve my understanding of fractions, percentages, and ratios?
A: Practice is key. Work through various problems, starting with simple ones and gradually increasing the complexity. Online resources, textbooks, and educational websites offer numerous practice exercises.
Conclusion: Mastering Fundamental Mathematical Concepts
The seemingly straightforward question, "What is 15 of 30?", provides a valuable opportunity to deepen your understanding of fundamental mathematical concepts. By exploring the problem through the lenses of fractions, percentages, and ratios, you not only find the answer (1/2, 50%, or 1:2) but also gain a broader appreciation for their interconnectedness and real-world applications. This foundational understanding will serve as a strong base for more advanced mathematical studies and will be invaluable in navigating various aspects of daily life and professional pursuits. Continue practicing and exploring these concepts, and you'll find yourself increasingly confident and proficient in mathematical reasoning.
Latest Posts
Latest Posts
-
3 5 Out Of 5 Percentage
Sep 13, 2025
-
Solve 1 4 5 4
Sep 13, 2025
-
2 1 7 As Improper Fraction
Sep 13, 2025
-
0 23 Acres To Square Feet
Sep 13, 2025
-
9 13 As A Decimal
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.