Whats 25 Percent Of 50
saludintensiva
Sep 23, 2025 · 5 min read
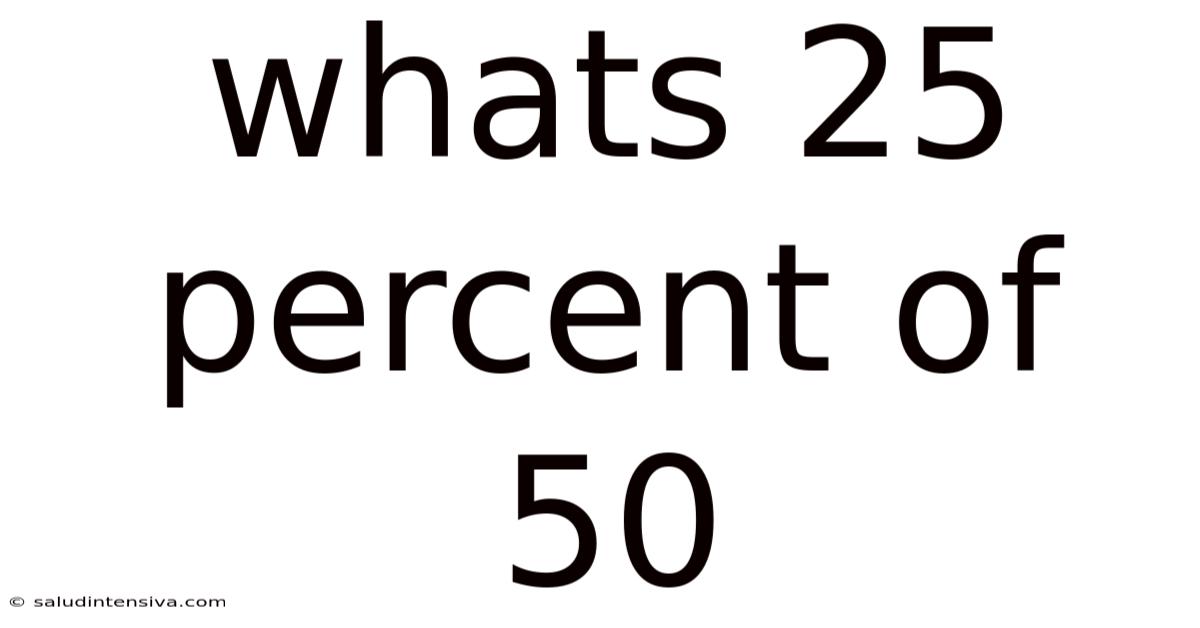
Table of Contents
What's 25 Percent of 50? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 50 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics: percentages. This article will not only answer the question directly but also explore the various methods for calculating percentages, delve into the underlying principles, and explore practical applications of this essential skill in everyday life and various fields. Understanding percentages is crucial for tasks ranging from calculating discounts in a store to analyzing financial statements. This comprehensive guide will equip you with the knowledge and confidence to tackle percentage problems with ease.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred" or "out of 100". When we say "25 percent," we mean 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25. This foundational understanding is key to tackling any percentage calculation.
Calculating 25 Percent of 50: Three Methods
There are several ways to calculate 25% of 50. Let's explore three common methods:
Method 1: Using the Fraction Equivalent
Since 25% is equivalent to the fraction 25/100, we can rewrite the problem as:
(25/100) * 50
This simplifies to:
(1/4) * 50 = 50/4 = 12.5
Therefore, 25% of 50 is 12.5.
Method 2: Using Decimal Equivalents
As mentioned earlier, 25% is equal to 0.25. We can therefore calculate 25% of 50 by multiplying 50 by 0.25:
0.25 * 50 = 12.5
This method is often preferred for its simplicity and ease of use with calculators.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between percentages and their corresponding values. We can set up a proportion:
25/100 = x/50
where 'x' represents the value we want to find (25% of 50). To solve for x, we cross-multiply:
25 * 50 = 100 * x
1250 = 100x
x = 1250/100 = 12.5
This method highlights the proportional relationship between the percentage and the whole value.
Beyond the Basics: Exploring Percentage Applications
The ability to calculate percentages extends far beyond simple arithmetic exercises. Let's explore some real-world applications:
1. Retail Discounts:
Imagine a shirt priced at $50 is on sale for 25% off. Using the methods described above, we know the discount is $12.50. The final price would be $50 - $12.50 = $37.50. This is a common calculation shoppers perform to determine the actual cost of items after discounts.
2. Tax Calculations:
Sales tax is often expressed as a percentage. If the sales tax in your area is 6%, and you purchase an item for $50, the tax amount would be 6% of $50, which is $3. The total cost, including tax, would be $50 + $3 = $53. Understanding percentage calculations ensures accurate tax calculations when making purchases.
3. Financial Investments:
Percentage calculations are essential in finance. For example, calculating interest earned on a savings account or investment returns often involves percentage calculations. Understanding percentage growth or decline is crucial for making informed financial decisions. If you invest $50 and it grows by 25%, your investment is now worth $62.50 ($50 + $12.50).
4. Data Analysis and Statistics:
Percentages are extensively used to represent data in various fields. Charts and graphs often utilize percentages to visualize proportions and trends within datasets. For instance, if 25% of survey respondents chose a particular option, this data is easily understood and compared to other response percentages.
5. Scientific Calculations and Research:
In scientific research and many scientific fields, percentages are crucial for expressing the concentration of solutions, the error margin in experiments, or the success rate of a particular process.
Advanced Percentage Calculations: Understanding Percentage Increase and Decrease
While calculating 25% of 50 is straightforward, let's consider more complex scenarios involving percentage increases and decreases.
Percentage Increase:
Suppose a value increases by a certain percentage. The formula for calculating the new value after a percentage increase is:
New Value = Original Value * (1 + Percentage Increase)
For example, if a value of 50 increases by 25%, the calculation would be:
New Value = 50 * (1 + 0.25) = 50 * 1.25 = 62.5
Percentage Decrease:
Similarly, if a value decreases by a certain percentage, the formula is:
New Value = Original Value * (1 - Percentage Decrease)
If a value of 50 decreases by 25%, the calculation would be:
New Value = 50 * (1 - 0.25) = 50 * 0.75 = 37.5
Solving for the Percentage: A Reverse Calculation
Sometimes, you might need to determine the percentage when the original value and the resulting value are known. Let's say a value increased from 50 to 62.5. To find the percentage increase:
- Calculate the difference: 62.5 - 50 = 12.5
- Divide the difference by the original value: 12.5 / 50 = 0.25
- Multiply by 100 to express as a percentage: 0.25 * 100 = 25%
Therefore, the value increased by 25%. This reverse calculation is useful in various situations, such as analyzing sales growth or determining the percentage change in a scientific experiment.
Frequently Asked Questions (FAQs)
Q: What if I need to calculate a percentage that's not a whole number, like 17.5%?
A: You can use the same methods described above, but instead of using the fraction 25/100, you would use the fraction 17.5/100 or the decimal 0.175.
Q: How can I easily calculate percentages without a calculator?
A: For simple percentages like 10%, 25%, or 50%, you can use mental math techniques. For example, 10% is simply moving the decimal point one place to the left. 25% can be calculated by finding one-fourth (dividing by 4). Practicing these techniques will improve your mental math skills.
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, numerous online percentage calculators are readily available. These tools can simplify complex calculations and provide quick results.
Conclusion: Mastering Percentages for Real-World Success
Calculating 25 percent of 50, which equals 12.5, is a starting point for understanding the broader world of percentages. This fundamental concept has wide-ranging applications in various aspects of life, from personal finance to professional fields. By mastering the different methods of calculation and understanding the underlying principles, you'll be well-equipped to tackle percentage problems with confidence and apply this essential skill to enhance your problem-solving abilities and decision-making in numerous real-world situations. Remember that consistent practice is key to mastering percentage calculations and solidifying your understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
70 Percent As A Decimal
Sep 23, 2025
-
1 75 As A Percent
Sep 23, 2025
-
How High Is 20 Meters
Sep 23, 2025
-
8712 Sq Ft To Acres
Sep 23, 2025
-
7 15 As A Percent
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.