X 2 Times X 4
saludintensiva
Sep 24, 2025 · 6 min read
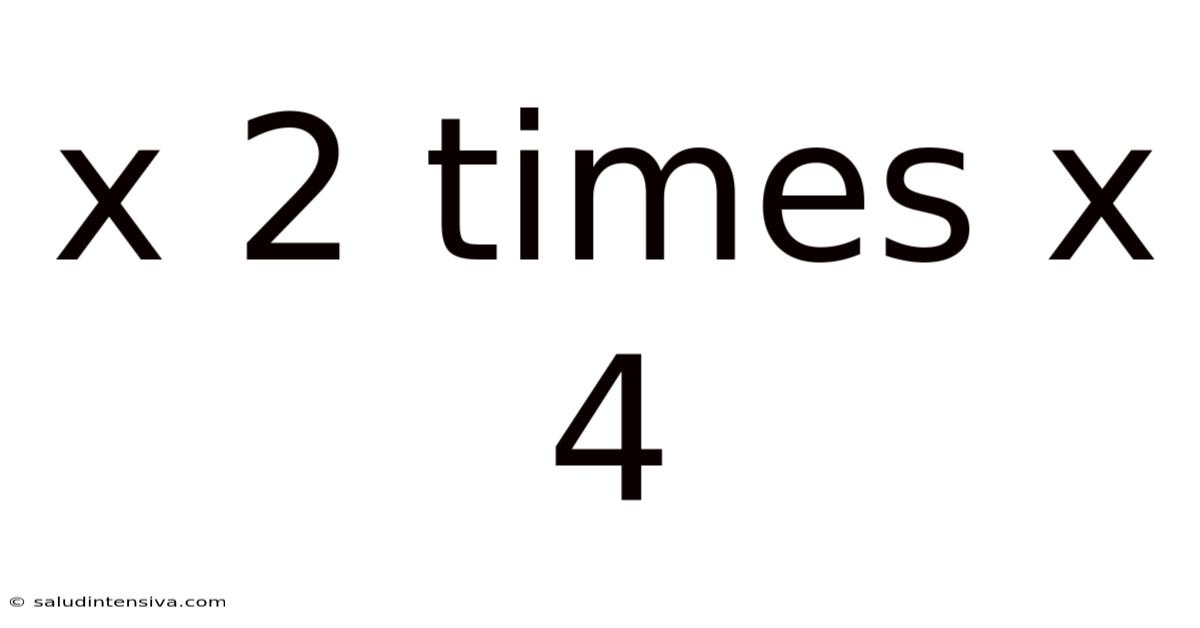
Table of Contents
Unlocking the Power of Repeated Multiplication: A Deep Dive into x2 x 4
This article explores the mathematical concept of repeated multiplication, specifically focusing on the expression "x 2 times x 4." We'll delve into its meaning, various interpretations, applications in different fields, and address common misconceptions. Understanding this seemingly simple concept opens doors to a deeper appreciation of algebra, exponents, and their widespread use in solving real-world problems.
Understanding the Fundamentals: Multiplication and Repeated Operations
Before we dive into the complexities (or lack thereof!) of "x 2 times x 4", let's solidify our understanding of the basic building blocks: multiplication. Multiplication is essentially a shorthand way of performing repeated addition. For example, 3 x 4 means adding three, four times: 3 + 3 + 3 + 3 = 12. This concept is crucial because it lays the foundation for understanding how repeated multiplication works.
The phrase "x 2 times" implies a multiplication operation repeated twice. Let's analyze what this means in the context of our problem. If we have "x 2 times x 4," we're dealing with two distinct multiplicative operations.
Interpreting "x 2 times x 4": Possible Scenarios
The ambiguity of the phrasing "x 2 times x 4" necessitates exploring different interpretations. The lack of explicit parentheses or other mathematical notation creates multiple valid interpretations, highlighting the importance of precise mathematical language. Here are the two most prominent ways to understand this expression:
Scenario 1: Sequential Multiplication
This interpretation treats the expression as two separate multiplication operations performed sequentially. We first multiply x by 2, and then multiply the result by 4. This can be represented algebraically as:
(x * 2) * 4
Simplifying this expression using the associative property of multiplication (which states that the grouping of factors doesn't affect the product), we get:
8x
This means that regardless of the value of x, the final result will always be eight times the value of x. For example, if x = 5, then (5 * 2) * 4 = 40, which is equal to 8 * 5.
Scenario 2: Exponentiation (Repeated Multiplication with a Single Base)
A second, less likely but still valid interpretation, considers the expression as implying repeated multiplication of the same base. Although the phrasing is not conventionally used for exponentiation, one could argue that "x 2 times x 4" suggests multiplying x by itself twice, then multiplying that result by 4. This would lead to a different outcome:
(x * x) * 4 = 4x²
This interpretation hinges on the ambiguous "x 2 times," which could be construed as x multiplied by itself twice (x²). However, this interpretation is less common and should be avoided unless explicitly stated or the context strongly suggests it. The first interpretation, sequential multiplication, is far more conventional and aligns with standard mathematical practice.
Applying Repeated Multiplication: Real-World Examples
The concept of repeated multiplication, as exemplified by our exploration of "x 2 times x 4," has far-reaching applications across diverse fields. Let's explore a few examples:
-
Compound Interest: In finance, compound interest involves earning interest not only on the principal amount but also on accumulated interest. The repeated multiplication inherent in compound interest calculations mirrors the structure of our problem. For instance, if an amount x earns interest at a rate of 2% annually for two years and 4% for the following year, the calculation involves sequential multiplication similar to Scenario 1.
-
Area Calculations: Consider calculating the area of a rectangular prism. If the length is x, the width is 2, and the height is 4, the volume would be (x * 2) * 4 = 8x, directly applying the logic of Scenario 1.
-
Geometric Progressions: A geometric progression is a sequence where each term is obtained by multiplying the previous term by a constant value. Understanding repeated multiplication is crucial for analyzing and working with geometric progressions. Many real-world phenomena, from population growth to radioactive decay, can be modeled using geometric progressions.
-
Computer Science: Repeated multiplication is fundamental in computer algorithms. Looping structures in programming languages often involve repeated application of an operation, which is analogous to repeated multiplication.
-
Physics and Engineering: Various physical phenomena involve exponential growth or decay, requiring the use of exponents (which are essentially repeated multiplication). This relates to Scenario 2 if we interpret "x 2 times" as x². Understanding this concept is crucial in areas like nuclear physics and circuit analysis.
The Importance of Precise Mathematical Notation
The ambiguity of "x 2 times x 4" underscores the vital role of precise mathematical notation. Using parentheses, exponents, and other symbolic representations removes ambiguity and ensures clarity in mathematical expressions. The proper way to represent Scenario 1 would be (x * 2) * 4, and for Scenario 2 (although less likely), it would be 4x². Clear notation prevents misunderstandings and allows for accurate calculations.
Extending the Concept: Exploring Exponents and Polynomials
The concept of repeated multiplication leads directly to the study of exponents. An exponent indicates how many times a base number is multiplied by itself. For example, x² means x * x. Our exploration of Scenario 2 touches upon this.
Further extending this, we can introduce the concept of polynomials. Polynomials are expressions that involve variables raised to non-negative integer powers and combined using addition, subtraction, and multiplication. Our simplified expression 8x is a simple example of a polynomial. More complex polynomials can involve multiple terms and higher exponents.
Frequently Asked Questions (FAQ)
Q: What is the definitive answer to "x 2 times x 4"?
A: There isn't a single definitive answer without additional context or clarification. The most common and mathematically sound interpretation is 8x (Scenario 1). However, a less conventional interpretation could lead to 4x² (Scenario 2). Proper mathematical notation is essential to remove this ambiguity.
Q: How do I avoid making similar mistakes in the future?
A: Always use precise mathematical notation. Parentheses are your friends! Clearly define your operations and ensure that your expressions are unambiguous. If there is any doubt, seek clarification.
Q: What are some other examples of repeated multiplication in everyday life?
A: Many everyday scenarios involve repeated multiplication. Think about doubling a recipe, calculating the total cost of multiple identical items, or determining the growth of a bacterial colony.
Q: How does this concept relate to higher-level mathematics?
A: Repeated multiplication forms the basis for many advanced mathematical concepts, including exponents, logarithms, calculus, and linear algebra. Understanding this fundamental concept is crucial for success in these fields.
Conclusion: Mastering the Fundamentals
The seemingly simple expression "x 2 times x 4" provides a valuable lesson in the importance of precise mathematical language and the power of repeated multiplication. While it presents two possible interpretations, highlighting the need for clear notation, the most likely and widely accepted solution is 8x. This exploration extends beyond a simple arithmetic problem, providing insights into exponents, polynomials, and the broader applications of repeated multiplication in numerous fields. Mastering this fundamental concept paves the way for a deeper understanding of more complex mathematical topics and their real-world applications. By understanding the nuances of repeated multiplication, you'll be better equipped to tackle more advanced mathematical challenges and contribute to innovative problem-solving in various disciplines.
Latest Posts
Latest Posts
-
Cube Root Function On Calculator
Sep 24, 2025
-
18 Degrees C In F
Sep 24, 2025
-
1 Million Divided By 50
Sep 24, 2025
-
1 5 Billion Divided By 100
Sep 24, 2025
-
Gcf Of 26 And 39
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about X 2 Times X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.