1 2 X 3 4
saludintensiva
Sep 17, 2025 · 6 min read
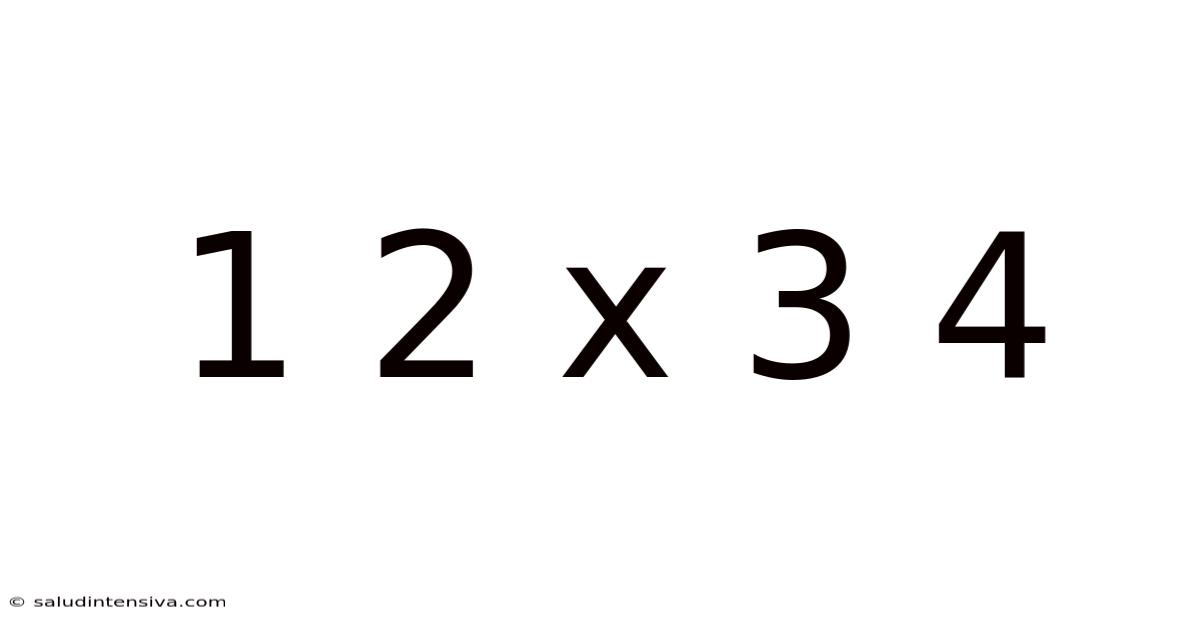
Table of Contents
Decoding the Seemingly Simple: Exploring the Mathematical and Philosophical Depths of "1 2 x 3 4"
This seemingly simple sequence of numbers, "1 2 x 3 4," presents a fascinating opportunity to delve into the world of mathematics, explore different interpretations, and even touch upon philosophical concepts of representation and meaning. While at first glance it might appear straightforward, a deeper look reveals layers of complexity and potential ambiguity, highlighting the importance of precise notation and understanding the context in which mathematical expressions are presented. This article will unpack this seemingly simple string of numbers, examining its potential interpretations, exploring underlying mathematical principles, and discussing the implications for clear communication in mathematics and beyond.
Understanding the Ambiguity: Order of Operations and Multiple Interpretations
The core challenge presented by "1 2 x 3 4" lies in its lack of explicit operators between the numbers. Without clear indications of addition, subtraction, division, or exponentiation, multiple interpretations are possible, leading to different results. This highlights the crucial role of the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction), or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). These mnemonics dictate the precedence of mathematical operations.
Interpretation 1: Sequential Multiplication
One possible interpretation is to treat the sequence as a continuous multiplication: 1 x 2 x 3 x 4. This results in a straightforward calculation:
1 x 2 = 2 2 x 3 = 6 6 x 4 = 24
Therefore, under this interpretation, "1 2 x 3 4" equals 24. This interpretation is arguably the most intuitive if one assumes a continuous operation.
Interpretation 2: Implicit Addition and Multiplication
Another interpretation involves treating the 'x' as an explicit multiplication operation only between '3' and '4', leaving the rest as implicit addition: 1 + 2 + (3 x 4). This yields:
3 x 4 = 12 1 + 2 + 12 = 15
Therefore, under this interpretation, "1 2 x 3 4" equals 15. This interpretation demonstrates the ambiguity that arises when operations are not explicitly defined.
Interpretation 3: Other Possible Interpretations (with added assumptions)
The lack of clear operators allows for even more creative, albeit less mathematically standard, interpretations. One could, for example, introduce exponentiation: (1 + 2)^3 x 4, which would give:
(1 + 2) = 3 3^3 = 27 27 x 4 = 108
This yields 108. Similarly, numerous other interpretations could be constructed depending on assumptions about the implied operations. However, it's crucial to note that these interpretations deviate from standard mathematical notation and emphasize the importance of clarity in expressing mathematical relationships.
The Importance of Precise Mathematical Notation
The ambiguity highlighted by the expression "1 2 x 3 4" underscores the paramount importance of precise mathematical notation. Without clearly defined operators and parentheses to guide the order of operations, the result of the expression becomes uncertain. This extends beyond simple arithmetic; clear notation is essential in all branches of mathematics, from algebra and calculus to advanced fields like topology and abstract algebra. Ambiguous notation can lead to errors, misunderstandings, and ultimately, incorrect conclusions.
Using parentheses or explicitly writing out the operations eliminates ambiguity. For instance, "(1 + 2) x (3 + 4)" or "1 + 2 x 3 + 4" are unambiguous and lead to specific, calculable results. The use of proper notation ensures that the intended meaning is conveyed accurately and removes the potential for multiple interpretations.
Connecting to Fundamental Mathematical Concepts
Even within the constraints of the ambiguous expression "1 2 x 3 4," we can connect to several fundamental mathematical concepts:
- Order of Operations: As discussed earlier, the ambiguity of the expression highlights the importance of understanding and correctly applying the order of operations. This is a cornerstone of arithmetic and algebraic manipulation.
- Factorials: While not directly present, the numbers 1, 2, 3, and 4 can be linked to the concept of factorials (!). The factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n. For example, 4! = 4 x 3 x 2 x 1 = 24. This connection, while not inherent to the original expression, illustrates the relationship between seemingly simple sequences and more complex mathematical structures.
- Sequences and Series: The numbers could be viewed as the initial terms of a sequence. The nature of this sequence (arithmetic, geometric, etc.) is unclear without further information, but this opens the door to discussions on patterns, progressions, and their applications in mathematics and other fields.
- Basic Arithmetic Operations: The expression fundamentally relies on the four basic arithmetic operations: addition, subtraction, multiplication, and division. Understanding these operations is foundational to all mathematical endeavors.
Beyond the Numbers: A Philosophical Perspective
The seemingly simple expression "1 2 x 3 4" can even be approached from a philosophical perspective. It raises questions about:
- Representation: How effectively do symbols represent mathematical concepts? The ambiguity of the expression highlights the limitations of simple symbolic representation without clear context.
- Meaning: Is meaning inherent in the symbols themselves, or does it depend entirely on the interpretation of the observer? The multiple interpretations of "1 2 x 3 4" suggest that meaning is not solely inherent but also relies on shared conventions and understandings.
- Communication: How critical is clear communication in conveying mathematical ideas? The expression serves as a stark reminder of the importance of precise and unambiguous language in mathematics and in any field requiring precise communication.
Frequently Asked Questions (FAQ)
-
Q: What is the "correct" answer to 1 2 x 3 4?
- A: There isn't a single "correct" answer without specifying the intended order of operations. The ambiguity of the expression allows for multiple interpretations, leading to different results (e.g., 24, 15, or other possibilities depending on added assumptions).
-
Q: Why is clear notation so important in mathematics?
- A: Clear notation prevents ambiguity and ensures that mathematical expressions are interpreted consistently. Without clear notation, mathematical communication breaks down, leading to errors and misunderstandings.
-
Q: Are there similar examples of ambiguous mathematical expressions?
- A: Yes, many expressions can be ambiguous without proper use of parentheses or clear indication of the order of operations. For example, "6/2(1+2)" is another example that leads to differing results based on individual interpretations of the order of operations.
-
Q: How can I avoid creating ambiguous mathematical expressions?
- A: Always use parentheses to clearly group operations and explicitly state all operators. This ensures that your intended meaning is clear and prevents misinterpretations.
Conclusion: The Power of Precision and Context
The simple sequence "1 2 x 3 4" serves as a powerful illustration of the importance of precision and context in mathematics. The ambiguity of the expression highlights the need for clear notation and the consistent application of the order of operations. Beyond the immediate mathematical calculations, it opens up avenues for exploring fundamental concepts and even delving into philosophical considerations of representation and meaning. This deceptively simple string of numbers serves as a valuable lesson in clear communication and the crucial role of context in interpreting mathematical expressions. Ultimately, the takeaway is that while exploration and different interpretations can be enriching, the bedrock of mathematics lies in precision and avoiding ambiguity through careful notation and clearly defined operations.
Latest Posts
Latest Posts
-
27 2 As A Mixed Number
Sep 17, 2025
-
Whats 20 Percent Of 13
Sep 17, 2025
-
Is 1 2 Greater Than 2 3
Sep 17, 2025
-
16 20 As A Percent
Sep 17, 2025
-
10 Out Of 12 Percent
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 2 X 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.