1 4 Divided By 2
saludintensiva
Sep 16, 2025 · 6 min read
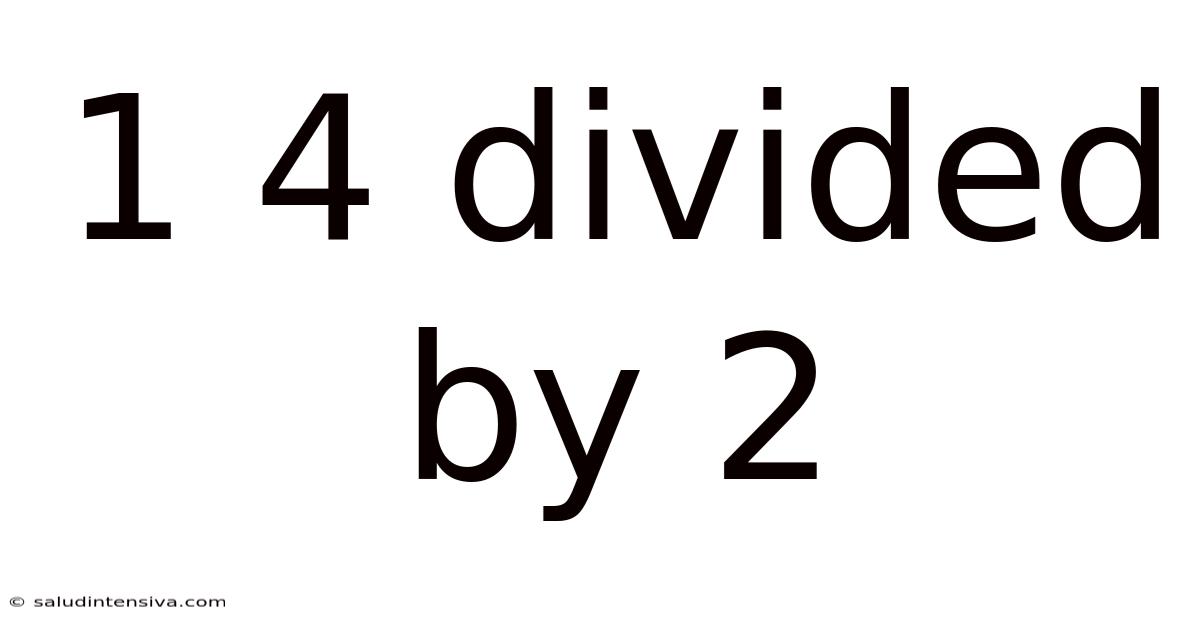
Table of Contents
Decoding 1/4 Divided by 2: A Deep Dive into Fraction Division
This article explores the seemingly simple yet fundamentally important mathematical concept of dividing fractions: specifically, 1/4 divided by 2. We'll move beyond a simple answer to understand the underlying principles, offering a comprehensive guide suitable for students of all levels, from elementary school to those brushing up on their foundational math skills. This will include practical examples, visual aids, and address common misconceptions to ensure a solid grasp of this crucial arithmetic operation.
Understanding Fractions: A Quick Refresher
Before diving into division, let's revisit the concept of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), such as 1/4. In this case, the numerator (1) indicates one part, and the denominator (4) indicates that the whole is divided into four equal parts.
Understanding fractions is paramount to comprehending fraction division. Think of a pizza cut into four equal slices. 1/4 represents one slice of that pizza. Now, let's explore what happens when we divide this slice further.
1/4 Divided by 2: The Calculation
The problem we're tackling is 1/4 ÷ 2. This means we're taking one-fourth of something and dividing it into two equal parts. Several methods can solve this:
Method 1: The "Keep, Change, Flip" Method (Reciprocal Method)
This is arguably the most popular and efficient method for dividing fractions. It involves three steps:
- Keep: Keep the first fraction (the dividend) as it is: 1/4.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (the divisor) – find its reciprocal. The reciprocal of 2 (which can be written as 2/1) is 1/2.
So, the problem becomes: 1/4 × 1/2.
Now, multiply the numerators together and the denominators together:
(1 × 1) / (4 × 2) = 1/8
Therefore, 1/4 divided by 2 equals 1/8.
Method 2: Visual Representation
Imagine our pizza slice (1/4). Dividing it by 2 means splitting that slice into two equal pieces. Each of these smaller pieces represents 1/8 of the whole pizza. This visual approach helps solidify the understanding of the mathematical operation.
Method 3: Using Decimal Equivalents
We can convert the fraction 1/4 to its decimal equivalent: 0.25. Then, we divide 0.25 by 2:
0.25 ÷ 2 = 0.125
Converting 0.125 back to a fraction, we get 1/8. This method reinforces the connection between fractions and decimals.
Understanding the Principles: Why Does "Keep, Change, Flip" Work?
The "keep, change, flip" method isn't just a trick; it's rooted in the fundamental principles of mathematics. Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by switching the numerator and the denominator.
Consider the expression a/b ÷ c/d. This can be rewritten as:
(a/b) × (d/c) = (a × d) / (b × c)
This is precisely what the "keep, change, flip" method does. It elegantly simplifies the process of dividing fractions.
Expanding the Concept: Dividing Fractions with Larger Numbers
Let's extend our understanding to more complex fraction divisions. Suppose we have the problem 3/5 ÷ 4/7. Following the "keep, change, flip" method:
- Keep: 3/5
- Change: ÷ becomes ×
- Flip: 4/7 becomes 7/4
The problem transforms into: 3/5 × 7/4 = (3 × 7) / (5 × 4) = 21/20
The result, 21/20, is an improper fraction (the numerator is larger than the denominator). It can be converted into a mixed number: 1 1/20.
Tackling Mixed Numbers in Division
Dividing fractions involving mixed numbers requires an extra step: converting the mixed numbers into improper fractions before applying the "keep, change, flip" method.
For instance, let's solve 1 1/2 ÷ 2/3:
- Convert mixed number to improper fraction: 1 1/2 = (1 × 2 + 1) / 2 = 3/2
- Apply "keep, change, flip": 3/2 ÷ 2/3 becomes 3/2 × 3/2
- Multiply: (3 × 3) / (2 × 2) = 9/4
- Convert back to a mixed number (if needed): 9/4 = 2 1/4
This demonstrates the process of handling mixed numbers within fraction division.
Real-World Applications of Fraction Division
Fraction division is far from an abstract mathematical concept; it finds practical application in numerous everyday situations:
- Cooking and Baking: Scaling recipes up or down requires dividing fractions. If a recipe calls for 1/4 cup of sugar, and you want to halve the recipe, you'll need to divide 1/4 by 2.
- Sewing and Crafting: Cutting fabric or other materials often involves precise fractional measurements and divisions.
- Construction and Engineering: Dividing fractional measurements is crucial for accurate calculations in construction and engineering projects.
- Data Analysis: Working with datasets often involves manipulating fractional data, including division.
Common Mistakes to Avoid
Several common pitfalls can hinder the understanding and accurate calculation of fraction division:
- Forgetting to flip the second fraction: This is the most common mistake. Remember the crucial "flip" step in the "keep, change, flip" method.
- Incorrectly converting mixed numbers: Ensure you correctly transform mixed numbers into improper fractions before proceeding with the division.
- Errors in multiplication: Carefully perform the multiplication of numerators and denominators to avoid simple arithmetic errors.
Frequently Asked Questions (FAQ)
Q: Can I divide a fraction by a whole number without using the "keep, change, flip" method?
A: Yes, you can. You can simply divide the numerator of the fraction by the whole number. For example, 1/4 ÷ 2 is the same as (1 ÷ 2) / 4 = 1/8. However, the "keep, change, flip" method is more versatile and applicable to all fraction divisions.
Q: What happens if the divisor is 0?
A: Division by zero is undefined in mathematics. It's an operation that does not yield a meaningful result.
Q: Are there other methods for dividing fractions besides "keep, change, flip"?
A: Yes, you can also use common denominators to divide fractions, but the "keep, change, flip" method is usually more straightforward.
Q: How do I divide a whole number by a fraction?
A: Treat the whole number as a fraction with a denominator of 1. For example, 3 ÷ 1/2 becomes 3/1 ÷ 1/2. Then apply the "keep, change, flip" method: 3/1 × 2/1 = 6.
Conclusion
Dividing fractions, even seemingly simple problems like 1/4 divided by 2, involves fundamental mathematical principles. Mastering this skill is crucial for success in higher-level mathematics and its real-world applications. The "keep, change, flip" method, supported by a strong understanding of fractions and their properties, provides an efficient and accurate approach to solving these problems. Remember to practice regularly and utilize visual aids to strengthen your comprehension and build confidence in tackling more complex fraction divisions. By understanding the underlying principles and avoiding common mistakes, you can conquer the world of fraction division with ease.
Latest Posts
Latest Posts
-
8 Years Ago From Today
Sep 16, 2025
-
22 Percent As A Fraction
Sep 16, 2025
-
3 4 X 1 6
Sep 16, 2025
-
Simplest Form Of 12 15
Sep 16, 2025
-
What Is 2 5 2 3
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1 4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.