13 18 As A Decimal
saludintensiva
Sep 17, 2025 · 6 min read
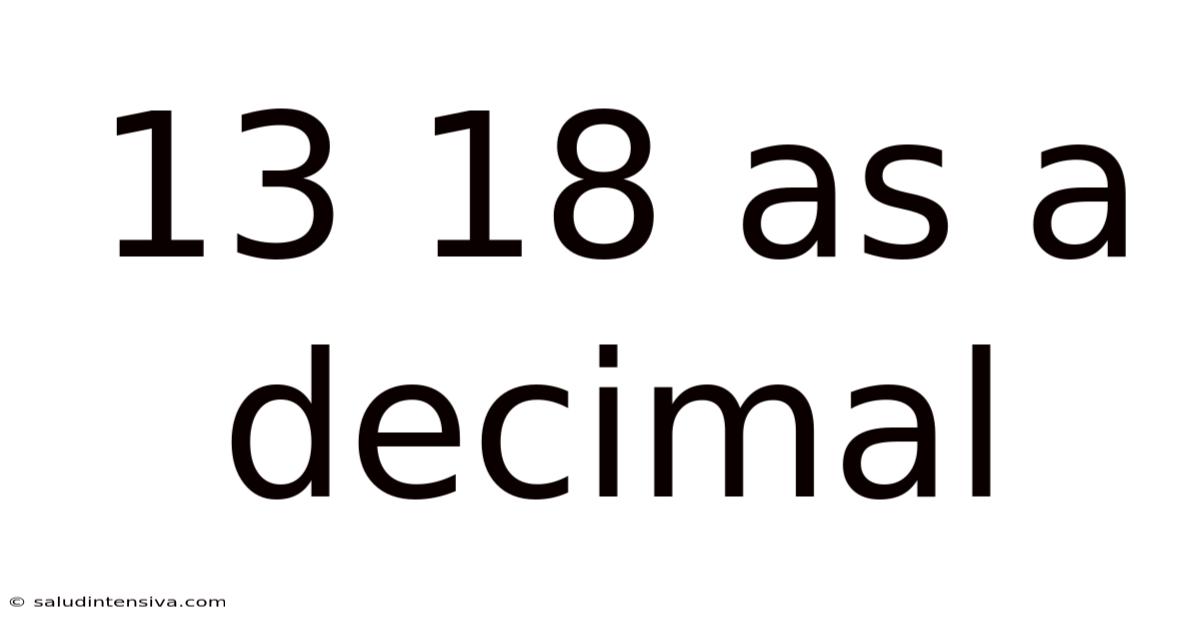
Table of Contents
Understanding 13/18 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This article provides a comprehensive guide to understanding how to convert the fraction 13/18 into a decimal, exploring various methods and delving into the underlying mathematical principles. We'll also address common misconceptions and answer frequently asked questions, making this a valuable resource for students and anyone seeking to strengthen their mathematical understanding. The keyword for this guide is fraction to decimal conversion, with supporting keywords like decimal representation, long division, repeating decimals, and fraction simplification.
Understanding Fractions and Decimals
Before we dive into converting 13/18, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a number using a base-ten system, with a decimal point separating the whole number part from the fractional part. Converting a fraction to a decimal essentially means expressing that part of a whole using the decimal system.
Method 1: Long Division
The most common and straightforward method for converting a fraction to a decimal is through long division. In this method, we divide the numerator (13) by the denominator (18).
Here's how to perform the long division for 13/18:
-
Set up the long division: Place the numerator (13) inside the division symbol and the denominator (18) outside. Since 13 is smaller than 18, we add a decimal point and a zero to 13, making it 13.0.
-
Perform the division: 18 goes into 130 seven times (18 x 7 = 126). Write the 7 above the decimal point in the quotient.
-
Subtract: Subtract 126 from 130, leaving a remainder of 4.
-
Bring down a zero: Bring down another zero from the right side, making the remainder 40.
-
Continue the division: 18 goes into 40 twice (18 x 2 = 36). Write the 2 in the quotient.
-
Subtract again: Subtract 36 from 40, leaving a remainder of 4.
-
Notice the pattern: At this point, you'll notice that the remainder is the same as before (4). This indicates that the decimal will repeat indefinitely.
Therefore, 13/18 as a decimal is approximately 0.7222... The '...' indicates that the digit 2 repeats infinitely. This is known as a repeating decimal or a recurring decimal.
Method 2: Using a Calculator
A simpler, albeit less insightful, method is to use a calculator. Simply input 13 ÷ 18 into your calculator. The result will display the decimal equivalent, likely showing a rounded-off version due to the calculator's display limitations. The calculator will show a result similar to 0.722222..., demonstrating the repeating nature of the decimal.
Understanding Repeating Decimals
The result of converting 13/18 to a decimal is a repeating decimal (0.7222...). This is because the denominator (18) contains prime factors other than 2 and 5. When a fraction's denominator contains prime factors other than 2 and 5, its decimal representation will be a repeating decimal. If the denominator only contains 2 and/or 5 as prime factors, the decimal will terminate (end after a finite number of digits). For example, 1/4 (denominator is 2²) is 0.25 (terminating decimal).
Representing Repeating Decimals
Repeating decimals can be represented in a couple of ways:
-
Using three dots (...): This indicates that the repeating pattern continues infinitely (e.g., 0.7222...).
-
Using a vinculum (¯): A line (vinculum) is placed above the repeating digits to show the repeating pattern (e.g., 0.7̅2̅). This is a more precise way of representing repeating decimals.
Why is 13/18 a Repeating Decimal?
The reason 13/18 results in a repeating decimal lies in the prime factorization of its denominator. The prime factorization of 18 is 2 x 3 x 3 (or 2 x 3²). Since the denominator contains a factor other than 2 or 5 (namely, 3), the decimal representation will be non-terminating and repeating.
Practical Applications
Understanding how to convert fractions to decimals is vital in various contexts:
-
Everyday Calculations: Dividing items equally, calculating percentages, or comparing proportions often involve converting fractions to decimals for easier understanding and calculations.
-
Financial Mathematics: Calculating interest rates, discounts, or profit margins often require converting fractions to decimals.
-
Science and Engineering: Many scientific and engineering calculations use decimals rather than fractions, making the conversion a necessary step in problem-solving.
-
Computer Programming: Computers often work with decimal representations of numbers, requiring programmers to understand fraction-to-decimal conversion.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be expressed as terminating decimals?
No. Only fractions whose denominators can be expressed solely as powers of 2 and/or 5 (or a combination thereof) will have terminating decimal representations. Other fractions will result in repeating decimals.
Q2: How can I simplify a fraction before converting it to a decimal?
Simplifying a fraction before converting to a decimal can make the long division process easier. Simplify by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. In this case, 13/18 is already in its simplest form because 13 and 18 share no common factors other than 1.
Q3: What is the difference between a terminating and a repeating decimal?
A terminating decimal ends after a finite number of digits (e.g., 0.25). A repeating decimal continues indefinitely with a repeating pattern of digits (e.g., 0.7222...).
Q4: Is there a way to predict if a fraction will have a repeating or terminating decimal representation?
Yes. If the denominator of the fraction, when simplified, contains only 2 and/or 5 as prime factors, the decimal will terminate. Otherwise, it will be a repeating decimal.
Q5: How do I convert a repeating decimal back to a fraction?
Converting a repeating decimal back to a fraction involves setting up an equation and solving for the unknown. This often involves multiplying the equation by powers of 10 to align the repeating digits and then subtracting the equations to eliminate the repeating part. This is a more advanced topic and requires a separate explanation.
Conclusion
Converting the fraction 13/18 to a decimal, whether through long division or using a calculator, demonstrates the fundamental principles of fraction-to-decimal conversion. Understanding the underlying reasons for repeating decimals, their representation, and their practical applications enriches one's mathematical understanding. This knowledge is crucial for various fields, emphasizing the significance of mastering this basic mathematical skill. Remember, practice makes perfect! The more you work with fractions and decimals, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
23 50 As A Decimal
Sep 17, 2025
-
Lcm Of 5 15 3
Sep 17, 2025
-
1 7 As A Percent
Sep 17, 2025
-
Can Percent Change Be Negative
Sep 17, 2025
-
Is 2 6 Equivalent To 4 12
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 13 18 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.