17/3 As A Mixed Number
saludintensiva
Sep 17, 2025 · 5 min read
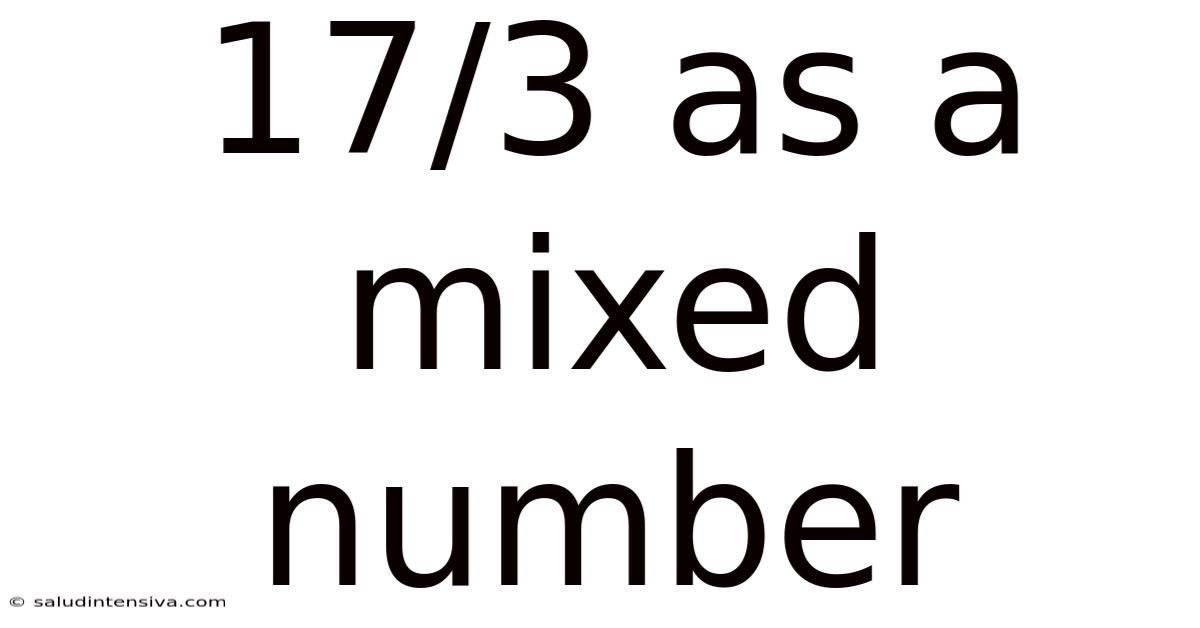
Table of Contents
Understanding 17/3 as a Mixed Number: A Comprehensive Guide
The fraction 17/3 represents seventeen thirds. While perfectly valid in its improper fraction form, understanding how to convert it into a mixed number is crucial for various mathematical operations and applications. This comprehensive guide will explore the concept of mixed numbers, detail the steps involved in converting 17/3, provide a scientific explanation behind the process, answer frequently asked questions, and finally, conclude with a summary of key takeaways. This exploration will equip you with a solid understanding of this fundamental mathematical concept.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number: it represents two whole units and three-quarters of another unit. Mixed numbers are a convenient way to represent quantities that are greater than one but not a whole number. They are often used in everyday situations, such as measuring ingredients in cooking or calculating lengths.
Converting 17/3 to a Mixed Number: A Step-by-Step Guide
Converting an improper fraction (where the numerator is larger than the denominator) like 17/3 into a mixed number involves a simple division process:
-
Divide the numerator by the denominator: Divide 17 by 3. This gives us 5 with a remainder of 2.
-
The quotient becomes the whole number: The result of the division (5) becomes the whole number part of our mixed number.
-
The remainder becomes the numerator of the fraction: The remainder (2) becomes the numerator of the fraction part of our mixed number.
-
The denominator remains the same: The denominator (3) remains unchanged in the fraction part of the mixed number.
Therefore, 17/3 as a mixed number is 5 ⅔.
Visualizing the Conversion
Imagine you have 17 equally sized pieces of pizza. If each whole pizza consists of 3 slices, how many whole pizzas and remaining slices do you have?
You can make 5 complete pizzas (5 x 3 = 15 slices used). You will have 2 slices remaining (17 - 15 = 2). So you have 5 whole pizzas and ⅔ of another pizza. This visually represents the conversion of 17/3 to 5 ⅔.
The Scientific Explanation: Understanding the Division Process
The process of converting an improper fraction to a mixed number is fundamentally rooted in the concept of division. When we divide 17 by 3, we are essentially determining how many times 3 fits completely into 17. The quotient represents the number of complete groups of 3, while the remainder represents the portion of a group that is left over.
This division operation can be expressed as:
17 ÷ 3 = 5 with a remainder of 2
This can be rewritten as:
17 = (3 x 5) + 2
This equation illustrates that 17 is composed of five groups of 3, plus an additional 2. The 5 groups represent the whole number part of our mixed number, and the remaining 2 forms the numerator of the fractional part, with the denominator remaining as 3. This clearly shows the mathematical foundation underlying the conversion process.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process: converting a mixed number back into an improper fraction. This is useful in various calculations and simplifying expressions. Let's use our example, 5 ⅔:
-
Multiply the whole number by the denominator: Multiply 5 (the whole number) by 3 (the denominator). This results in 15.
-
Add the numerator: Add the result (15) to the numerator (2). This gives 17.
-
Keep the denominator the same: The denominator remains 3.
Therefore, 5 ⅔ converts back to 17/3. This demonstrates the equivalence between the mixed number and the improper fraction representation.
Frequently Asked Questions (FAQ)
Q1: Why is it important to know how to convert between improper fractions and mixed numbers?
A: Converting between improper fractions and mixed numbers is crucial for several reasons. First, it allows for easier visualization and understanding of quantities greater than one. Second, it simplifies calculations, particularly when dealing with addition, subtraction, multiplication, and division of fractions. Third, it's essential for solving real-world problems involving measurements, proportions, and other quantitative concepts.
Q2: Can all improper fractions be converted to mixed numbers?
A: Yes, every improper fraction can be converted to a mixed number. The process involves dividing the numerator by the denominator, and the result will always yield a whole number part and a fractional part (unless the fraction is already a whole number).
Q3: What if the remainder is 0 after the division?
A: If the remainder is 0, it means the improper fraction is actually a whole number. For example, if we had 18/3, we'd get 6 with a remainder of 0. This means 18/3 is simply 6.
Q4: Are there any other ways to represent 17/3?
A: While 5 ⅔ is the most common and practical representation, 17/3 could also be represented as a decimal (5.666...), but the mixed number offers a more precise and easily understandable representation in many contexts.
Q5: How does this relate to other mathematical concepts?
A: Understanding mixed numbers and their relationship to improper fractions is fundamental to more advanced mathematical concepts, including algebra, geometry, and calculus. It forms the foundation for working with rational numbers and solving equations involving fractions.
Conclusion: Mastering the Conversion of 17/3
Converting the improper fraction 17/3 to the mixed number 5 ⅔ is a fundamental skill in arithmetic. This guide has detailed the step-by-step process, provided a visual representation, and explored the underlying mathematical principles. Understanding this conversion is not merely about memorizing a procedure; it's about grasping the relationship between fractions, whole numbers, and division. This understanding forms a crucial building block for more advanced mathematical concepts and problem-solving. Mastering this seemingly simple conversion will significantly enhance your mathematical proficiency and confidence in tackling more complex problems in the future. Remember the core principle: division is the key, and the result—the whole number and the remaining fraction—provides the mixed number equivalent.
Latest Posts
Latest Posts
-
10 2 X 3
Sep 18, 2025
-
What Is Half Of 54
Sep 18, 2025
-
Is 2 3 Greater Than 2 8
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 17/3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.