2/3 + 1/4 In Fraction
saludintensiva
Sep 14, 2025 · 6 min read
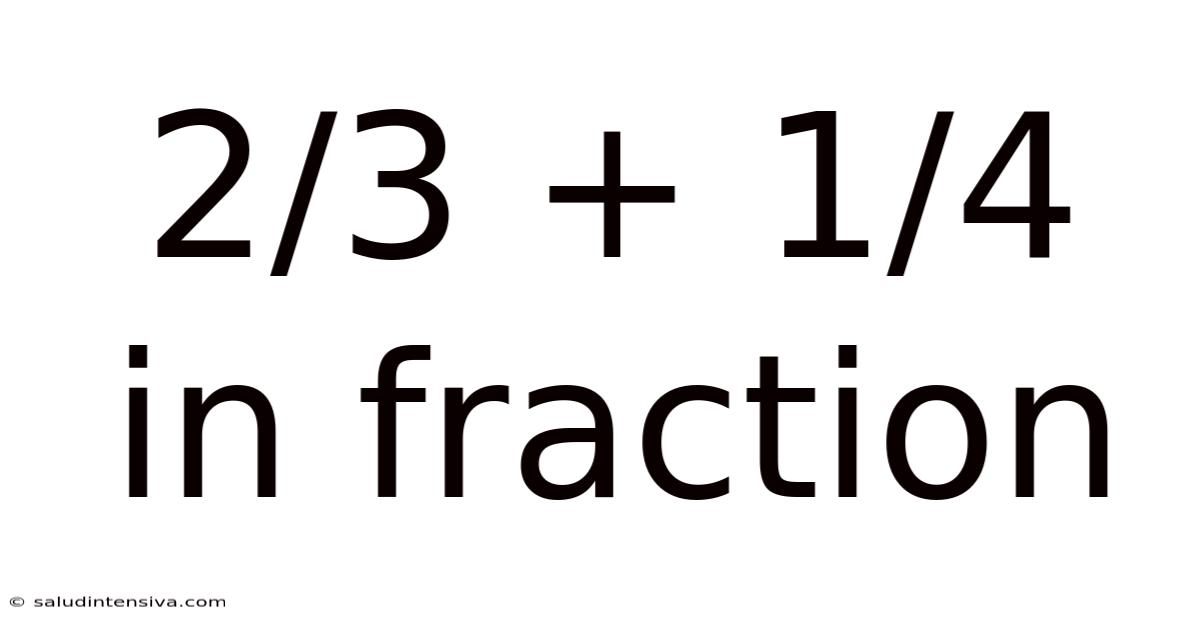
Table of Contents
Mastering Fractions: A Comprehensive Guide to Adding 2/3 + 1/4
Adding fractions might seem daunting at first, especially when the denominators (the bottom numbers) are different. But fear not! This comprehensive guide will walk you through adding 2/3 and 1/4, explaining the process step-by-step, revealing the underlying mathematical principles, and answering frequently asked questions. By the end, you'll not only know the answer but also understand why the method works, empowering you to tackle any fraction addition problem with confidence.
Introduction: Understanding Fractions
Before diving into the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), like this: a/b. The numerator tells us how many parts we have, and the denominator tells us how many equal parts the whole is divided into. For example, 1/2 means one out of two equal parts, or one-half.
In our problem, 2/3 + 1/4, we are adding two fractions with different denominators. This is where the concept of finding a common denominator comes into play. This is crucial because we can only add or subtract fractions when they share the same denominator. Think of it like adding apples and oranges – you can't simply add them together unless you convert them into a common unit, like "fruit."
Finding the Least Common Denominator (LCD)
The least common denominator (LCD) is the smallest number that both denominators (3 and 4 in this case) can divide into evenly. There are a few ways to find the LCD:
-
Listing Multiples: List the multiples of each denominator until you find the smallest number that appears in both lists.
- Multiples of 3: 3, 6, 9, 12, 15, 18...
- Multiples of 4: 4, 8, 12, 16, 20... The smallest number common to both lists is 12. Therefore, the LCD of 3 and 4 is 12.
-
Prime Factorization: This method is particularly useful for larger numbers. Break down each denominator into its prime factors (numbers divisible only by 1 and themselves).
- 3 = 3 (3 is a prime number)
- 4 = 2 x 2 To find the LCD, take the highest power of each prime factor present in either factorization and multiply them together. In this case, we have 2² and 3. So, LCD = 2 x 2 x 3 = 12.
Converting Fractions to a Common Denominator
Now that we have the LCD (12), we need to convert both fractions so they have this denominator. We do this by multiplying both the numerator and the denominator of each fraction by the same number. This doesn't change the value of the fraction, as we're essentially multiplying by 1 (e.g., 2/2 = 1).
-
Converting 2/3: To get a denominator of 12, we need to multiply the denominator (3) by 4. Therefore, we must also multiply the numerator (2) by 4: (2/3) x (4/4) = 8/12
-
Converting 1/4: To get a denominator of 12, we need to multiply the denominator (4) by 3. Therefore, we must also multiply the numerator (1) by 3: (1/4) x (3/3) = 3/12
Adding the Fractions
Now that both fractions have the same denominator (12), we can add them simply by adding the numerators and keeping the denominator the same:
8/12 + 3/12 = (8 + 3)/12 = 11/12
Therefore, 2/3 + 1/4 = 11/12
Simplifying Fractions (if necessary)
Sometimes, after adding fractions, the resulting fraction can be simplified. This means reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). In this case, 11 and 12 have no common divisors other than 1, so 11/12 is already in its simplest form.
Visual Representation: Understanding the Process
Imagine a pizza cut into 12 slices. 2/3 of the pizza would be 8 slices (2/3 * 12 = 8), and 1/4 of the pizza would be 3 slices (1/4 * 12 = 3). If you add the 8 slices from the 2/3 portion and the 3 slices from the 1/4 portion, you get 11 slices out of a total of 12. This visually represents 11/12.
The Mathematical Explanation: Why This Works
The process of finding a common denominator and then adding the numerators is based on the fundamental principle of equivalent fractions. When we multiply the numerator and denominator of a fraction by the same number, we are essentially multiplying the fraction by 1 (which doesn't change its value). This allows us to express both fractions with the same denominator, making the addition straightforward.
The addition of fractions with a common denominator is simply adding the number of parts we have (numerators). Since the sizes of the parts are the same (represented by the common denominator), the sum directly represents the combined number of parts.
Step-by-Step Guide for Adding Fractions with Different Denominators
-
Find the Least Common Denominator (LCD): Use the methods described above (listing multiples or prime factorization) to determine the smallest common multiple of the denominators.
-
Convert Fractions to Equivalent Fractions with the LCD: Multiply the numerator and denominator of each fraction by the appropriate number to achieve the LCD.
-
Add the Numerators: Keep the denominator the same and add the numerators together.
-
Simplify (if possible): Reduce the resulting fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
Frequently Asked Questions (FAQs)
-
What if I choose a common denominator that is not the least common denominator? You'll still get the correct answer, but you'll end up with a larger fraction that will need to be simplified. Using the LCD makes the simplification process easier.
-
Can I add fractions with different signs (positive and negative)? Yes, you follow the same steps, but remember the rules for adding and subtracting integers. For example, 2/3 + (-1/4) would be solved by finding the LCD and then performing the subtraction: 8/12 - 3/12 = 5/12.
-
What if the fractions are mixed numbers (a whole number and a fraction)? Convert the mixed numbers into improper fractions (where the numerator is larger than the denominator) before adding them using the same steps as above. For example, 1 1/3 + 2 1/4 would first be converted to 4/3 and 9/4, then proceed with finding the LCD and adding.
Conclusion: Mastering Fraction Addition
Adding fractions might seem challenging initially, but with a systematic approach and a good understanding of the underlying concepts, it becomes straightforward. By mastering the steps of finding the least common denominator, converting fractions, and simplifying the result, you’ll gain the confidence to tackle any fraction addition problem, regardless of the complexity of the denominators. Remember the pizza analogy – visualize the fractions and the addition process to reinforce your understanding. With practice, you'll become proficient in this fundamental mathematical skill. So grab your pencil and paper, and start practicing! You've got this!
Latest Posts
Latest Posts
-
26 Acre To Sq Ft
Sep 14, 2025
-
12 Percent As A Fraction
Sep 14, 2025
-
What Does 3 5 Equal
Sep 14, 2025
-
What Time Is 18 44
Sep 14, 2025
-
6 Divided By 1 4
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2/3 + 1/4 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.