25 Percent As A Fraction
saludintensiva
Sep 18, 2025 · 5 min read
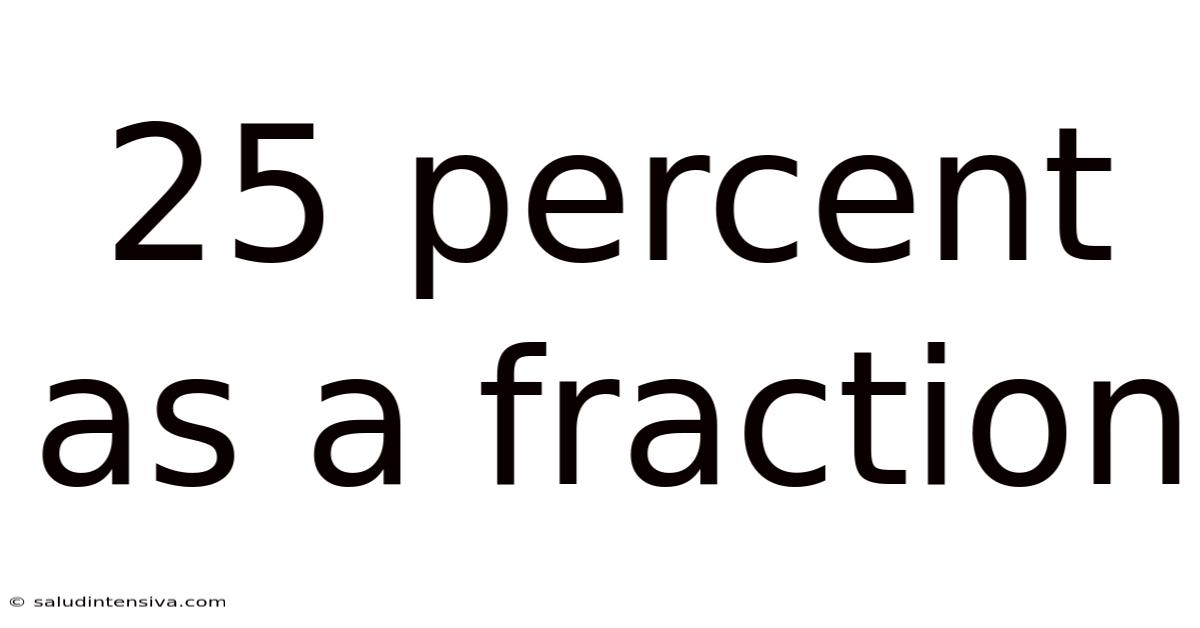
Table of Contents
25 Percent as a Fraction: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics, crucial for everyday life and various academic disciplines. This article delves deep into the concept of representing 25 percent as a fraction, exploring its different forms, applications, and related mathematical principles. We'll cover everything from basic conversions to more advanced applications, ensuring a thorough understanding for readers of all levels. By the end, you'll not only know how to express 25% as a fraction but also gain a broader perspective on percentage-to-fraction conversions.
Understanding Percentages and Fractions
Before diving into the specifics of 25%, let's establish a firm understanding of percentages and fractions. A percentage represents a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 25% literally means 25 out of 100.
A fraction, on the other hand, expresses a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into.
Converting 25% to a Fraction: The Basic Method
The simplest way to convert 25% to a fraction is to directly translate its meaning: 25 out of 100. This gives us the fraction 25/100.
25% = 25/100
This fraction, while correct, isn't in its simplest form. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. The GCD of 25 and 100 is 25. Dividing both the numerator and denominator by 25, we get:
25/100 = 1/4
Therefore, 25% expressed as a fraction in its simplest form is 1/4.
Different Representations of 25% as a Fraction
While 1/4 is the most common and simplest representation, 25% can be expressed as other equivalent fractions. This is achieved by multiplying both the numerator and the denominator of the simplified fraction by the same number. For example:
- Multiplying by 2: (1/4) * (2/2) = 2/8
- Multiplying by 3: (1/4) * (3/3) = 3/12
- Multiplying by 4: (1/4) * (4/4) = 4/16
- And so on...
All these fractions (2/8, 3/12, 4/16, etc.) are equivalent to 1/4 and, therefore, represent 25%. However, 1/4 is the simplest and most commonly used representation.
Practical Applications of 25% as a Fraction (1/4)
The fraction 1/4, representing 25%, appears frequently in various contexts:
- Discount Calculations: A 25% discount means you pay 75% (or 3/4) of the original price. Understanding this as 1/4 helps in quick mental calculations.
- Proportions and Ratios: Many problems involving proportions and ratios utilize fractions. Representing 25% as 1/4 simplifies such calculations.
- Data Analysis: When analyzing data presented as percentages, converting to fractions often aids in comparisons and interpretations.
- Geometry and Measurement: 1/4 is often used to represent portions of shapes, angles, and measurements. For example, a quarter of a circle is 1/4 of the whole circle.
- Cooking and Baking: Recipes frequently use fractions, and understanding 25% as 1/4 is valuable for adjusting ingredient quantities.
Converting Other Percentages to Fractions
The method used for converting 25% to a fraction can be applied to any percentage. Here's a step-by-step guide:
- Write the percentage as a fraction with a denominator of 100. For example, 70% becomes 70/100.
- Simplify the fraction. Find the greatest common divisor (GCD) of the numerator and denominator and divide both by it. For 70/100, the GCD is 10, resulting in the simplified fraction 7/10.
- The simplified fraction represents the percentage. 70% is equivalent to 7/10.
Let's try another example: 60%
- 60% = 60/100
- The GCD of 60 and 100 is 20.
- 60/100 ÷ 20/20 = 3/5
Therefore, 60% is equivalent to 3/5.
Working with Decimal Representations
Percentages can also be easily converted to decimals. To convert a percentage to a decimal, simply divide the percentage by 100. For 25%, this would be 25 ÷ 100 = 0.25. Decimals and fractions are closely related; 0.25 is equivalent to 25/100, which simplifies to 1/4. This conversion allows for seamless transitions between percentages, fractions, and decimals in various mathematical operations.
Advanced Applications: Percentage Increase and Decrease
Understanding 25% as a fraction is crucial when dealing with percentage increases or decreases. For example, if a price increases by 25%, we can calculate the new price by adding 1/4 of the original price to the original price. Similarly, if a price decreases by 25%, we subtract 1/4 of the original price from the original price.
Frequently Asked Questions (FAQ)
Q1: Is 1/4 the only fraction representing 25%?
A1: No, while 1/4 is the simplest form, infinitely many equivalent fractions represent 25% (e.g., 2/8, 3/12, 4/16, and so on). However, 1/4 is preferred due to its simplicity.
Q2: How do I convert a fraction to a percentage?
A2: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100. For example, to convert 1/4 to a percentage: (1 ÷ 4) x 100 = 25%.
Q3: What if I have a percentage with a decimal, like 25.5%?
A3: You can treat it the same way. 25.5% becomes 25.5/100. You can then simplify by multiplying by 10 to get 255/1000. Then you can simplify this fraction by finding the GCD. In this case, the GCD is 5, so 255/1000 simplifies to 51/200.
Q4: Are there any shortcuts for converting common percentages to fractions?
A4: Yes, memorizing the fractional equivalents of common percentages (like 25% = 1/4, 50% = 1/2, 75% = 3/4, etc.) can significantly speed up calculations.
Conclusion
Understanding how to represent 25% as a fraction, and more generally, converting between percentages and fractions, is a fundamental mathematical skill with wide-ranging applications. Mastering this concept empowers you to solve problems involving discounts, proportions, ratios, data analysis, and more. By grasping the underlying principles and practicing conversion techniques, you can confidently navigate various mathematical scenarios where percentages and fractions are involved. Remember, the simplest representation of 25% as a fraction is 1/4, but understanding equivalent fractions provides a more comprehensive grasp of the concept. This knowledge forms a strong foundation for more advanced mathematical pursuits.
Latest Posts
Latest Posts
-
Is 2 3 More Than 3 4
Sep 18, 2025
-
18 Out Of 25 Percentage
Sep 18, 2025
-
7 6 As A Mixed Number
Sep 18, 2025
-
Convert 0 5 To A Fraction
Sep 18, 2025
-
What Is 2 3 Plus 2 3
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 25 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.