3 12 As A Percent
saludintensiva
Sep 14, 2025 · 5 min read
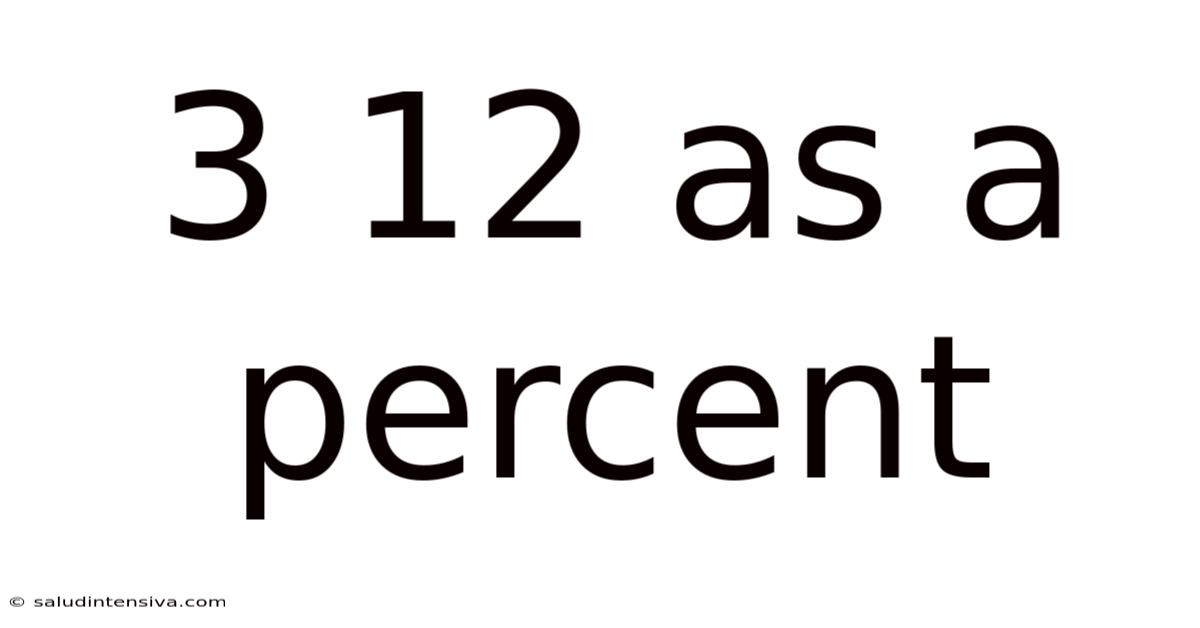
Table of Contents
Understanding 3/12 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday calculations. This article will thoroughly explore how to express the fraction 3/12 as a percentage, explaining the process step-by-step and delving into the underlying concepts. We will cover different methods, address common misconceptions, and provide practical examples to solidify your understanding. This comprehensive guide will leave you confident in converting fractions to percentages and applying this knowledge to real-world scenarios.
Introduction: Fractions, Decimals, and Percentages – A Unified Perspective
Before diving into the specific conversion of 3/12, let's establish a clear understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For example, 3/12 indicates 3 parts out of a total of 12 parts.
-
Decimal: A decimal is a way of expressing a number using base-10, with a decimal point separating the whole number part from the fractional part. Decimals are particularly useful for calculations and comparisons.
-
Percentage: A percentage represents a fraction or decimal as a portion of 100. The symbol "%" denotes "per hundred," signifying that the number represents a proportion out of 100.
These three forms are interchangeable. Understanding their relationship is crucial for tackling various mathematical problems. Converting between them involves simple arithmetic operations.
Method 1: Simplifying the Fraction Before Conversion
The fraction 3/12 can be simplified before converting it to a percentage. Simplification involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD of 3 and 12 is 3.
- Simplification: 3/12 ÷ 3/3 = 1/4
Now, we have a simplified fraction, 1/4. This makes the conversion to a percentage easier.
-
Conversion to Decimal: To convert the fraction 1/4 to a decimal, divide the numerator (1) by the denominator (4): 1 ÷ 4 = 0.25
-
Conversion to Percentage: To convert the decimal 0.25 to a percentage, multiply by 100: 0.25 × 100 = 25%
Therefore, 3/12 simplifies to 1/4, which is equivalent to 0.25 or 25%.
Method 2: Direct Conversion from Fraction to Percentage
This method involves directly converting the fraction 3/12 to a percentage without simplifying it first.
-
Conversion to Decimal: Divide the numerator (3) by the denominator (12): 3 ÷ 12 = 0.25
-
Conversion to Percentage: Multiply the decimal by 100: 0.25 × 100 = 25%
This method yields the same result as the simplification method, demonstrating that simplification is a matter of preference and doesn't alter the final answer.
Method 3: Using Proportions
Another approach uses the concept of proportions. We can set up a proportion to find the equivalent percentage:
- Set up the proportion: 3/12 = x/100
Here, 'x' represents the percentage we need to find. To solve for 'x', cross-multiply:
-
Cross-multiplication: 12x = 300
-
Solve for x: x = 300 ÷ 12 = 25
Therefore, 3/12 is equal to 25%. This method reinforces the underlying principle of percentages as a proportion out of 100.
Understanding the Concept: What Does 25% Really Mean?
25% means 25 parts out of 100 equal parts. Imagine a pizza cut into 100 slices. 25% of the pizza would be 25 of those slices. This visualization helps solidify the concept of percentages as proportions.
Practical Applications: Real-World Examples of 3/12 (or 25%)
The conversion of 3/12 to 25% has numerous practical applications:
-
Sales Discounts: A 25% discount on a $100 item means a reduction of $25 (25% of $100).
-
Grade Calculations: If you answer 3 out of 12 questions correctly on a quiz, your score is 25%.
-
Financial Calculations: Interest rates, tax calculations, and investment returns often involve percentages. Understanding the conversion from fractions to percentages is essential for financial literacy.
-
Data Analysis: Representing data in percentages allows for easy comparison and interpretation. For instance, if 3 out of 12 survey respondents prefer a particular product, this translates to a 25% preference rate.
Common Misconceptions and Troubleshooting
A common mistake is forgetting to multiply the decimal by 100 when converting to a percentage. Remember, a percentage is always expressed as a value out of 100.
Another potential issue is incorrectly simplifying the fraction. Always ensure you find the greatest common divisor to simplify completely.
Finally, some individuals might struggle with the division step involved in converting the fraction to a decimal. Practice with various fractions will improve your proficiency.
Frequently Asked Questions (FAQ)
Q: Can I convert any fraction to a percentage?
A: Yes, any fraction can be converted to a percentage using the methods described above.
Q: What if the fraction is an improper fraction (numerator > denominator)?
A: An improper fraction, when converted to a decimal, will result in a decimal greater than 1. Multiplying this decimal by 100 will yield a percentage greater than 100%. This is perfectly valid and represents a proportion exceeding 100%.
Q: Are there any online tools or calculators to assist with fraction-to-percentage conversions?
A: While numerous online calculators can perform this conversion, understanding the underlying process is crucial for developing mathematical proficiency and problem-solving skills. Using a calculator should be supplementary to understanding the manual conversion method.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting 3/12 to a percentage, whether through simplification or direct conversion, consistently yields 25%. This seemingly simple calculation underscores the fundamental interconnectedness of fractions, decimals, and percentages. Mastering this skill is not only essential for academic success but also equips you with practical tools for navigating various aspects of daily life and professional endeavors. Remember, practice is key. Work through various examples, and you'll soon find these conversions second nature. The ability to confidently move between these different numerical representations empowers you to tackle more complex mathematical challenges with increased ease and understanding.
Latest Posts
Latest Posts
-
Tattoo Font Generator Roman Numerals
Sep 14, 2025
-
What Is Equal To 4 3
Sep 14, 2025
-
4 10 In Simplest Form
Sep 14, 2025
-
Is 3 16 Smaller Than 1 4
Sep 14, 2025
-
Is 1 2 Bigger Than 2 3
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3 12 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.