3 2 As Mixed Number
saludintensiva
Sep 17, 2025 · 7 min read
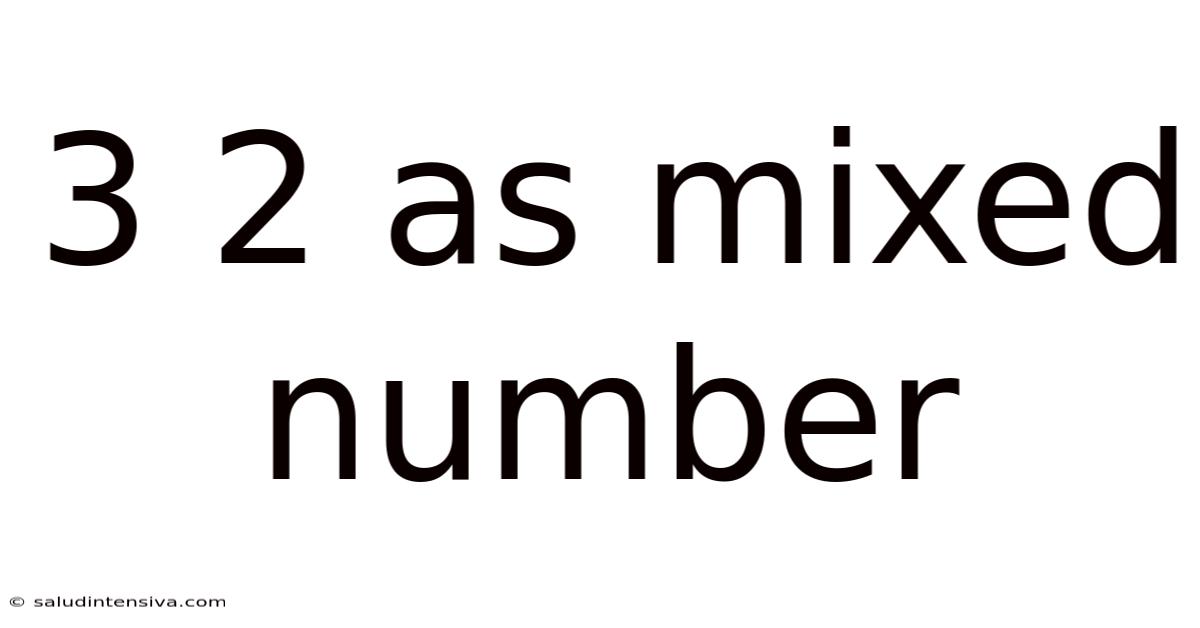
Table of Contents
Understanding 3 2: Demystifying Mixed Numbers
Mixed numbers, a cornerstone of arithmetic, often present a hurdle for students transitioning from whole numbers to fractions. This comprehensive guide will delve into the intricacies of mixed numbers, focusing specifically on the representation and manipulation of "3 2". While the expression itself might seem incomplete or erroneous (as it lacks an explicit fractional component), we'll explore its potential interpretations and related concepts within the broader context of fractional arithmetic. We'll examine how to represent this expression correctly, explore its relationship to improper fractions, and provide practical examples to solidify your understanding.
What are Mixed Numbers?
A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator (top number) smaller than its denominator (bottom number), indicating a portion of a whole. For instance, 2 ½ represents two whole units and one-half of another. The key to understanding mixed numbers lies in recognizing that the whole number and the fraction are added together to represent a single quantity.
Interpreting "3 2" : The Missing Fraction
The expression "3 2" as it stands is incomplete as a mixed number. It needs a fractional component to make sense within the context of mixed numbers. The '3' clearly indicates three whole units. However, the '2' requires clarification. Is it:
-
A whole number added to 3? If so, the correct representation would be 5 (3 + 2 = 5). This is a straightforward addition of whole numbers, not involving mixed numbers.
-
The numerator of a fraction? If this is the case, a denominator is missing. We need to know the fractional part, e.g., 3 ⅔, 3 ²/₅, or 3 ²/₁₀. The missing denominator significantly alters the meaning and value of the expression.
-
Part of a larger mathematical expression? "3 2" might be part of a more complex equation or problem requiring further context for proper interpretation.
Let's assume the "2" is intended to be the numerator of a fraction. We'll proceed by exploring a few possibilities with different denominators to illustrate how this changes the mixed number:
Examples with Different Denominators
To fully understand the implications of a missing denominator, let's consider a few scenarios:
1. 3 ⅔: This represents three whole units and two-thirds of another. To convert this to an improper fraction (where the numerator is greater than or equal to the denominator), we follow these steps:
- Multiply the whole number by the denominator: 3 x 3 = 9
- Add the numerator: 9 + 2 = 11
- Keep the same denominator: 3 ⅔ = ¹¹⁄₃
2. 3 ²/₅: This represents three whole units and two-fifths of another. Converting to an improper fraction:
- Multiply the whole number by the denominator: 3 x 5 = 15
- Add the numerator: 15 + 2 = 17
- Keep the same denominator: 3 ²/₅ = ¹⁷⁄₅
3. 3 ²/₁₀: This represents three whole units and two-tenths of another. Converting to an improper fraction:
- Multiply the whole number by the denominator: 3 x 10 = 30
- Add the numerator: 30 + 2 = 32
- Keep the same denominator: 3 ²/₁₀ = ³²/₁₀
As you can see, the value of the mixed number dramatically changes based on the chosen denominator. This highlights the critical importance of complete and unambiguous notation in mathematics.
Converting Improper Fractions to Mixed Numbers
The reverse process—converting an improper fraction to a mixed number—is equally important. Let's use the examples above to demonstrate:
1. Converting ¹¹⁄₃ to a mixed number:
- Divide the numerator by the denominator: 11 ÷ 3 = 3 with a remainder of 2
- The quotient (3) becomes the whole number.
- The remainder (2) becomes the numerator of the fraction.
- The denominator remains the same (3).
- Therefore, ¹¹⁄₃ = 3 ⅔
2. Converting ¹⁷⁄₅ to a mixed number:
- Divide the numerator by the denominator: 17 ÷ 5 = 3 with a remainder of 2
- The quotient (3) becomes the whole number.
- The remainder (2) becomes the numerator of the fraction.
- The denominator remains the same (5).
- Therefore, ¹⁷⁄₅ = 3 ²/₅
3. Converting ³²/₁₀ to a mixed number:
- Divide the numerator by the denominator: 32 ÷ 10 = 3 with a remainder of 2
- The quotient (3) becomes the whole number.
- The remainder (2) becomes the numerator of the fraction.
- The denominator remains the same (10).
- Therefore, ³²/₁₀ = 3 ²/₁₀
This conversion process is fundamental to working with fractions and mixed numbers effectively.
Adding and Subtracting Mixed Numbers
Once you have a correctly written mixed number, you can perform arithmetic operations. Let's consider adding and subtracting mixed numbers, using our previous examples:
Adding: Let's add 3 ⅔ and 2 ½:
- Convert to improper fractions: 3 ⅔ = ¹¹⁄₃ and 2 ½ = ⁵⁄₂
- Find a common denominator: The least common multiple of 3 and 2 is 6.
- Convert fractions to have the common denominator: ¹¹⁄₃ = ²²/₆ and ⁵⁄₂ = ¹⁵⁄₆
- Add the fractions: ²²/₆ + ¹⁵⁄₆ = ³⁷⁄₆
- Convert the improper fraction back to a mixed number: ³⁷⁄₆ = 6 ¹⁄₆
Subtracting: Let's subtract 2 ½ from 3 ⅔:
- Convert to improper fractions: 3 ⅔ = ¹¹⁄₃ and 2 ½ = ⁵⁄₂
- Find a common denominator: The least common multiple of 3 and 2 is 6.
- Convert fractions to have the common denominator: ¹¹⁄₃ = ²²/₆ and ⁵⁄₂ = ¹⁵⁄₆
- Subtract the fractions: ²²/₆ - ¹⁵⁄₆ = ⁷⁄₆
- Convert the improper fraction back to a mixed number: ⁷⁄₆ = 1 ¹⁄₆
These examples showcase the standard procedures for adding and subtracting mixed numbers. Remember that consistent application of these steps is crucial for accuracy.
Multiplying and Dividing Mixed Numbers
Multiplying and dividing mixed numbers involves similar steps, but with slight variations:
Multiplying: To multiply mixed numbers, it's generally easier to first convert them into improper fractions. Let's multiply 3 ⅔ by 2 ½:
- Convert to improper fractions: 3 ⅔ = ¹¹⁄₃ and 2 ½ = ⁵⁄₂
- Multiply the numerators and denominators: (¹¹ x ⁵) / (3 x 2) = ⁵⁵⁄₆
- Convert the improper fraction back to a mixed number: ⁵⁵⁄₆ = 9 ¹⁄₆
Dividing: Division of mixed numbers also benefits from conversion to improper fractions. Let's divide 3 ⅔ by 2 ½:
- Convert to improper fractions: 3 ⅔ = ¹¹⁄₃ and 2 ½ = ⁵⁄₂
- Invert the second fraction (reciprocal) and multiply: ¹¹⁄₃ x ²⁄₅ = ²²/₁₅
- Convert the improper fraction back to a mixed number: ²²/₁₅ = 1 ⁷⁄₁₅
These examples demonstrate that converting to improper fractions simplifies the multiplication and division processes, avoiding complexities of working directly with whole numbers and fractions simultaneously.
Frequently Asked Questions (FAQ)
Q: What happens if I get a remainder of zero when converting an improper fraction to a mixed number?
A: If you get a remainder of zero, it means the improper fraction is actually a whole number. For example, ⁶⁄₃ = 2 (because 6 ÷ 3 = 2 with no remainder).
Q: Is there a shortcut for converting mixed numbers to improper fractions?
A: Yes, a useful shortcut involves multiplying the whole number by the denominator, adding the numerator, and keeping the same denominator. This is the same process outlined earlier, just condensed.
Q: Why is it important to use a common denominator when adding or subtracting fractions?
A: We need a common denominator because you can only add or subtract parts of the same whole. Imagine trying to add apples and oranges – you need to express them in a common unit before combining them. Similarly, fractions must have a common denominator to represent parts of the same whole unit.
Q: Can I multiply or divide mixed numbers without converting them to improper fractions?
A: While technically possible, it's far more complex and prone to errors. Converting to improper fractions simplifies the calculation significantly.
Q: What if the expression "3 2" is meant to represent something entirely different, outside of mixed numbers?
A: Context is key. If "3 2" is encountered in a broader mathematical context (like coordinates, a matrix, or a different type of notation), its interpretation depends entirely on the specific application or problem being solved. Mathematical notation varies between fields.
Conclusion
Understanding mixed numbers is essential for proficiency in arithmetic. The expression "3 2," while seemingly incomplete, highlights the importance of clear and unambiguous notation. By exploring different interpretations based on potential denominators, we've demonstrated how a missing fractional component significantly alters the value and meaning of the expression. Through various examples of conversion between mixed numbers and improper fractions, along with practical illustrations of addition, subtraction, multiplication, and division, this guide aims to solidify your understanding of mixed numbers and their manipulation. Remember to always check your work and ensure the clarity of your mathematical notation to avoid errors and misunderstandings. The principles discussed here provide a solid foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
27 Out Of 30 Percent
Sep 17, 2025
-
Gcf Of 72 And 24
Sep 17, 2025
-
4 Divided By Negative 2
Sep 17, 2025
-
3 5 Simplified As A Fraction
Sep 17, 2025
-
1 2 Minus 1 4
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 2 As Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.