3 5 Divided By 2
saludintensiva
Sep 14, 2025 · 6 min read
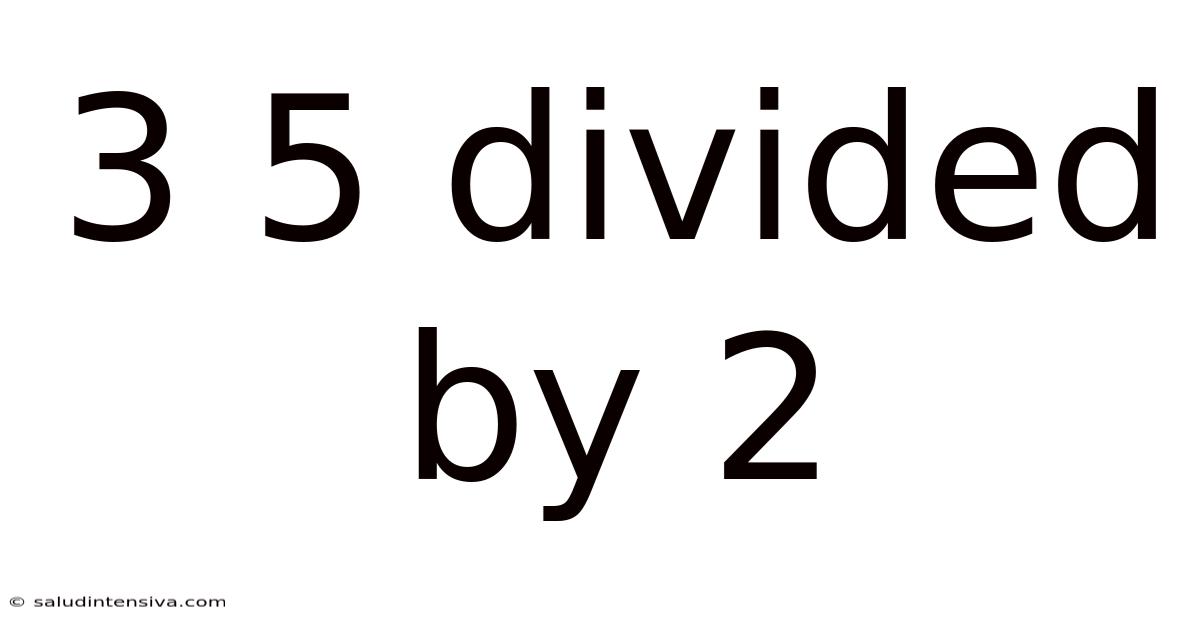
Table of Contents
Decoding 35 Divided by 2: A Deep Dive into Division and its Applications
Understanding division is fundamental to mathematics and numerous real-world applications. This article will explore the seemingly simple problem of 35 divided by 2, delving far beyond the basic answer to uncover the underlying principles, different approaches to solving it, and its significance in various contexts. We will explore both the process of long division and the concept of remainders, connecting these mathematical concepts to practical scenarios. By the end, you'll not only know the answer but also possess a deeper understanding of division itself.
Understanding the Problem: 35 ÷ 2
The problem "35 divided by 2" (written as 35 ÷ 2 or 35/2) asks: how many times does 2 fit into 35? This simple question opens the door to a world of mathematical concepts. We'll initially focus on two primary methods of solving this: long division and using fractions.
Method 1: Long Division – A Step-by-Step Guide
Long division is a systematic method for dividing larger numbers. Let's break down the process for 35 ÷ 2:
-
Setup: Write the problem as:
_____ 2 | 35 -
Divide the tens digit: How many times does 2 go into 3? It goes in once (2 x 1 = 2). Write the "1" above the 3 in the quotient.
1___ 2 | 35 -
Subtract: Subtract the result (2) from the tens digit (3): 3 - 2 = 1.
1___ 2 | 35 -2 --- 1 -
Bring down the ones digit: Bring down the ones digit (5) next to the remainder (1).
1___ 2 | 35 -2 --- 15 -
Divide the new number: How many times does 2 go into 15? It goes in 7 times (2 x 7 = 14). Write the "7" above the 5 in the quotient.
17__ 2 | 35 -2 --- 15 -
Subtract again: Subtract the result (14) from 15: 15 - 14 = 1. This is our remainder.
17__ 2 | 35 -2 --- 15 -14 --- 1 -
Interpreting the result: The quotient is 17, and the remainder is 1. This means 2 goes into 35 seventeen times with one left over. We can express this as 17 with a remainder of 1, or as a mixed number (17 1/2), or as a decimal (17.5).
Method 2: Fractions and Decimals
The problem 35 ÷ 2 can also be expressed as the fraction 35/2. To solve this:
-
Improper Fraction to Mixed Number: We can convert the improper fraction (35/2) into a mixed number. We divide the numerator (35) by the denominator (2). The quotient (17) becomes the whole number part, and the remainder (1) becomes the numerator of the fraction, keeping the denominator (2). This gives us 17 1/2.
-
Fraction to Decimal: To convert the fraction 1/2 to a decimal, we perform the division: 1 ÷ 2 = 0.5. Therefore, 35/2 = 17.5
Both methods yield the same result: 35 divided by 2 equals 17 with a remainder of 1, which is equivalent to 17 1/2 or 17.5.
Understanding Remainders: More Than Just Leftovers
The remainder (1 in this case) is a crucial part of the answer. It signifies the portion of 35 that isn't perfectly divisible by 2. Remainders are not simply "leftovers"; they hold significant meaning depending on the context of the problem.
-
Real-world examples: If you have 35 apples and want to divide them equally among 2 people, each person gets 17 apples, and there's 1 apple left over.
-
Further calculations: The remainder can be crucial in further calculations. For instance, in modular arithmetic (used in cryptography and computer science), the remainder is the key element.
-
Rounding: Depending on the situation, you might round the answer up or down. In the apple example, you might give the extra apple to one person or divide it in half.
The Significance of Decimal Representation: 17.5
The decimal representation (17.5) provides a more precise answer, particularly useful when dealing with quantities that can be divided into fractional parts (e.g., money, weight, volume). It represents the exact value of 35/2, avoiding the need for expressing the remainder separately.
Applications of Division in Real-World Scenarios
The seemingly simple operation of division underpins a vast array of real-world applications:
-
Sharing equally: Dividing resources (money, food, tasks) among people or groups.
-
Calculating averages: Finding the average of a set of numbers.
-
Scaling recipes: Adjusting the quantities of ingredients in a recipe to serve more or fewer people.
-
Unit conversions: Converting between different units of measurement (e.g., kilometers to miles).
-
Ratio and proportion: Solving problems involving ratios and proportions.
-
Geometry and measurement: Calculating areas, volumes, and other geometric properties.
-
Financial calculations: Calculating interest, profit margins, and other financial metrics.
-
Computer programming: Division is a fundamental operation used extensively in programming for various calculations and data manipulation.
-
Engineering and physics: Division is used in numerous engineering and physics calculations, from determining the speed of an object to calculating forces.
Exploring Further: Division with Larger Numbers and Decimals
The principles discussed for 35 ÷ 2 apply to divisions involving larger numbers and decimals. The process remains the same, although the calculations might become more complex. For decimal division, you'll need to handle decimal points carefully, often involving shifting decimal points to make the divisor a whole number.
Frequently Asked Questions (FAQ)
-
Q: What if the remainder is zero?
- A: If the remainder is zero, it means the number is perfectly divisible by the divisor. For example, 36 ÷ 2 = 18 (remainder 0).
-
Q: How do I handle division with larger numbers?
- A: The process of long division remains the same, but the calculations become more involved. You'll need to follow the same steps systematically, ensuring accuracy in each step of the subtraction and division.
-
Q: How do I handle division with decimals?
- A: For decimal division, it's often helpful to make the divisor a whole number by multiplying both the divisor and dividend by the same power of 10. Then, proceed with long division as usual. Remember to adjust the decimal point in the quotient accordingly.
-
Q: What are some real-world examples of division besides sharing equally?
- A: Many applications involve calculating rates, speeds, averages, ratios, and proportions. For example, calculating miles per gallon for a car, determining the average speed of a journey, or finding the unit price of an item are all based on the principle of division.
Conclusion: Beyond the Simple Answer
While the answer to 35 divided by 2 is simply 17 with a remainder of 1 (or 17.5), this article aimed to illuminate the deeper mathematical concepts involved. We've explored different approaches, highlighted the significance of remainders, and discussed various real-world applications. Understanding division is not just about finding a numerical answer; it's about grasping the fundamental principles that underpin numerous mathematical operations and their relevance in solving problems across diverse fields. Hopefully, this in-depth exploration has broadened your understanding of this seemingly simple yet powerful mathematical operation.
Latest Posts
Latest Posts
-
Is 3 16 Smaller Than 1 4
Sep 14, 2025
-
Is 1 2 Bigger Than 2 3
Sep 14, 2025
-
What Is 25 Of 14000
Sep 14, 2025
-
Hcf Of 12 And 15
Sep 14, 2025
-
2 1 3 In Decimal
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3 5 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.