4 5 In Simplest Form
saludintensiva
Sep 12, 2025 · 6 min read
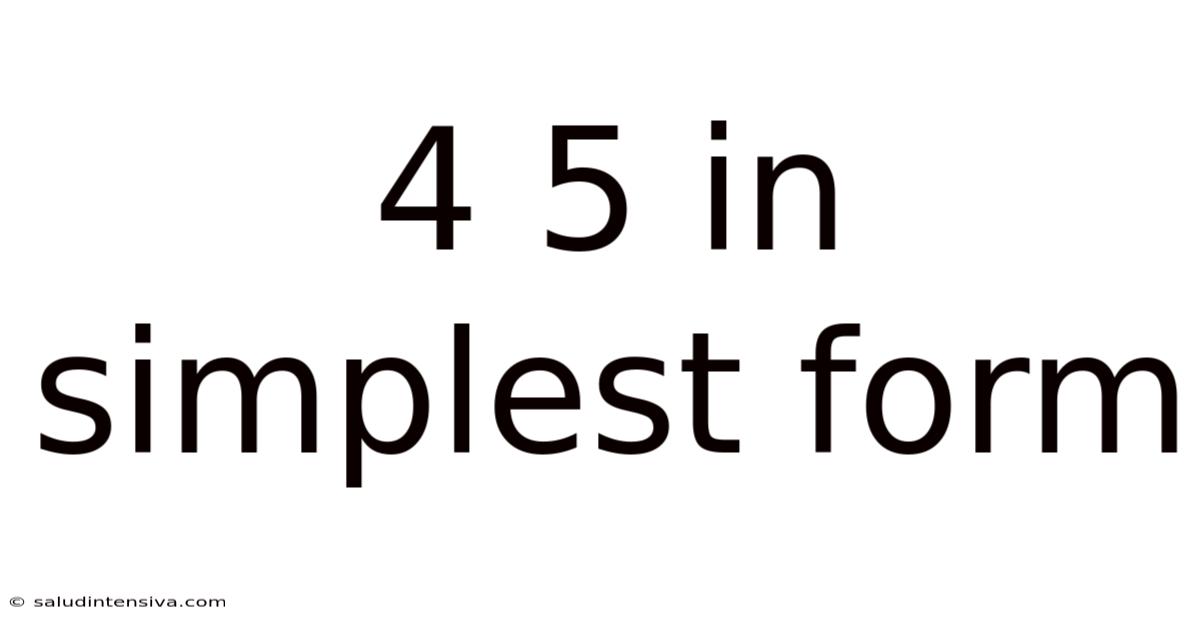
Table of Contents
Simplifying Fractions: Understanding 4/5 in its Simplest Form
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to advanced calculus. This article will delve into the concept of simplifying fractions, using the example of 4/5, and explore why it's already in its simplest form. We'll cover the process of simplification, explore the underlying mathematical principles, and address common questions surrounding this seemingly simple yet vital concept.
Introduction: What are Fractions and Why Simplify?
A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the top number) and 'b' is the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, and the numerator tells us how many of those parts we have.
Simplifying a fraction, also known as reducing a fraction to its lowest terms, means expressing the fraction in its most concise form without changing its value. This makes it easier to understand, compare, and use in calculations. We simplify a fraction by finding the greatest common divisor (GCD) – the largest number that divides both the numerator and the denominator evenly – and dividing both by that number.
Why 4/5 is Already in its Simplest Form
The fraction 4/5 is already in its simplest form because the numerator (4) and the denominator (5) have no common factors other than 1. In other words, their greatest common divisor (GCD) is 1. Let's explore this concept further.
To find the GCD of two numbers, we can use several methods:
-
Listing Factors: List all the factors of both numbers and identify the largest number that appears in both lists. The factors of 4 are 1, 2, and 4. The factors of 5 are 1 and 5. The only common factor is 1.
-
Prime Factorization: Express each number as a product of its prime factors (numbers divisible only by 1 and themselves). Then, identify the common prime factors and multiply them together to find the GCD. The prime factorization of 4 is 2 x 2. The prime factorization of 5 is just 5. Since there are no common prime factors, the GCD is 1.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD. For 4 and 5, we would do:
5 ÷ 4 = 1 with a remainder of 1. 4 ÷ 1 = 4 with a remainder of 0.
The last non-zero remainder is 1, therefore the GCD is 1.
Since the GCD of 4 and 5 is 1, dividing both the numerator and denominator by 1 doesn't change the fraction's value. Therefore, 4/5 remains 4/5, and it's considered to be in its simplest form.
Illustrative Examples: Simplifying Other Fractions
Let's look at some examples where simplifying is necessary:
-
12/18: The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The greatest common divisor is 6. Dividing both numerator and denominator by 6 gives us 2/3.
-
20/25: The prime factorization of 20 is 2 x 2 x 5. The prime factorization of 25 is 5 x 5. The greatest common divisor is 5. Dividing both by 5 gives us 4/5. Notice this simplified fraction is now in its simplest form.
-
15/35: The factors of 15 are 1, 3, 5, and 15. The factors of 35 are 1, 5, 7, and 35. The GCD is 5. Dividing both by 5, we get 3/7.
These examples demonstrate how the process of finding the GCD is crucial for simplifying fractions to their lowest terms.
The Importance of Simplifying Fractions
Simplifying fractions offers several key advantages:
-
Clarity: Simplified fractions are easier to understand and interpret. 2/3 is much clearer than 12/18.
-
Comparison: Comparing simplified fractions is simpler. It's easier to see that 2/3 is greater than 1/2 than it is to compare 12/18 and 9/18.
-
Calculations: Simplifying fractions before performing calculations (addition, subtraction, multiplication, and division) can significantly reduce the complexity and chance of errors.
Beyond the Basics: Equivalent Fractions
Understanding that simplifying a fraction doesn't change its value is linked to the concept of equivalent fractions. Equivalent fractions are fractions that represent the same proportion or part of a whole. For example, 1/2, 2/4, 3/6, 4/8, and so on, are all equivalent fractions. Simplifying a fraction is essentially finding the equivalent fraction with the smallest whole-number numerator and denominator.
Real-World Applications of Fractions
Fractions are ubiquitous in everyday life:
-
Cooking and Baking: Recipes often use fractional measurements (e.g., 1/2 cup of sugar, 2/3 cup of flour).
-
Measurement: Many measurements involve fractions (e.g., inches, feet, meters).
-
Money: Understanding fractions is important for working with cents (1 cent is 1/100 of a dollar).
-
Probability: Probability is often expressed using fractions (e.g., the probability of flipping heads is 1/2).
-
Data Analysis: Fractions are used extensively in data analysis and statistics.
Frequently Asked Questions (FAQ)
-
Q: What if I don't know how to find the greatest common divisor (GCD)?
A: There are various methods, as explained above: listing factors, prime factorization, and the Euclidean algorithm. For simple fractions, listing factors is often sufficient. For larger numbers, the Euclidean algorithm is more efficient. Many calculators also have a GCD function.
-
Q: Can a fraction be simplified if the numerator is 1?
A: Yes, but only if the denominator is also 1. If the numerator is 1, the fraction is already in its simplest form unless the denominator is also 1 (which equals 1).
-
Q: Is there a way to simplify fractions quickly?
A: With practice and familiarity with prime numbers and divisibility rules, you'll become faster at simplifying. Using prime factorization can also speed up the process.
-
Q: Why is simplifying fractions important in higher-level mathematics?
A: In algebra and calculus, simplified fractions make equations and expressions easier to manipulate and solve. They are essential for simplifying complex calculations and avoiding unnecessary computational steps.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill in mathematics with broad applications across various fields. While the fraction 4/5 is already in its simplest form, understanding the process of simplification and its underlying principles is crucial for working effectively with fractions of all kinds. Mastering this skill will enhance your mathematical abilities and confidence, paving the way for success in more advanced mathematical concepts. The ability to identify the greatest common divisor quickly and efficiently is key to this process, and with practice, this will become second nature. Remember, the goal is not just to get the right answer but also to understand why the answer is correct – this understanding is the foundation for future mathematical success.
Latest Posts
Latest Posts
-
5 9 In Decimal Form
Sep 12, 2025
-
8 9 Divided By 4
Sep 12, 2025
-
What Is 2 10 Simplified
Sep 12, 2025
-
Is 7 16 Bigger Than 1 2
Sep 12, 2025
-
20 3 As A Mixed Number
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 4 5 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.