5 Out Of 25 Percentage
saludintensiva
Sep 16, 2025 · 6 min read
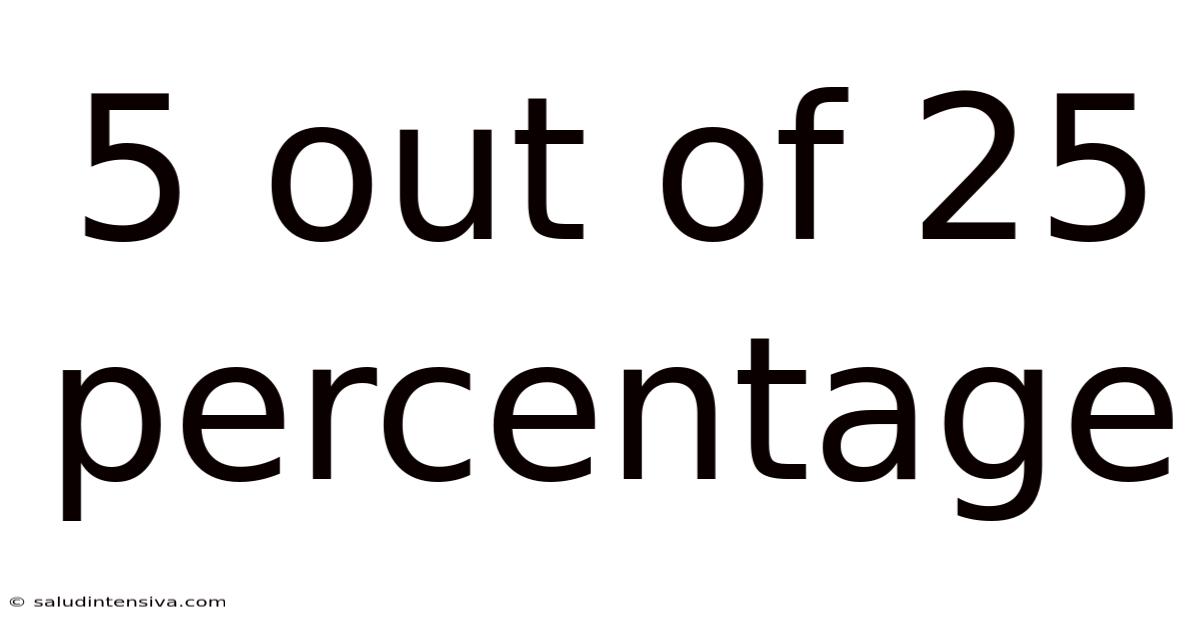
Table of Contents
Understanding 5 out of 25: Percentages, Fractions, and Their Real-World Applications
Calculating percentages is a fundamental skill applicable across numerous aspects of life, from academic assessments to financial management and everyday problem-solving. This article delves deep into understanding the concept of "5 out of 25," explaining its representation as a fraction, a decimal, and, most importantly, a percentage. We'll explore the various methods for calculating this and similar scenarios, along with practical examples to solidify your comprehension. By the end, you'll not only understand how to calculate 5 out of 25 as a percentage but also grasp the broader principles behind percentage calculations.
Understanding Fractions and Percentages
Before diving into the specifics of 5 out of 25, let's establish a firm understanding of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 5/25, 5 is the numerator and 25 is the denominator. This fraction indicates that we're considering 5 parts out of a total of 25 parts.
A percentage, on the other hand, is a way of expressing a fraction as a portion of 100. The symbol "%" signifies "per cent" or "out of 100". Therefore, a percentage represents how many parts out of 100 make up the whole. Converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100, or using a simple calculation.
Calculating 5 out of 25 as a Percentage: Three Methods
There are several ways to calculate the percentage represented by 5 out of 25. Let's examine three common approaches:
Method 1: Simplifying the Fraction
The simplest method involves simplifying the fraction 5/25 to its lowest terms. Both the numerator and the denominator are divisible by 5:
5 ÷ 5 = 1 25 ÷ 5 = 5
This simplifies the fraction to 1/5. Now, to convert this fraction to a percentage, we need to find an equivalent fraction with a denominator of 100. We can achieve this by multiplying both the numerator and the denominator by 20:
(1 × 20) / (5 × 20) = 20/100
Therefore, 20/100 represents 20%. Thus, 5 out of 25 is equal to 20%.
Method 2: Direct Conversion Using Division
This method involves dividing the numerator (5) by the denominator (25) and then multiplying the result by 100 to express it as a percentage:
(5 ÷ 25) × 100 = 0.2 × 100 = 20%
This directly converts the fraction to a decimal (0.2) and then to a percentage (20%).
Method 3: Using Proportions
This method uses the concept of proportions to solve for the percentage. We can set up a proportion:
5/25 = x/100
where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
25x = 500
x = 500 ÷ 25 = 20
Therefore, x = 20%, confirming that 5 out of 25 is 20%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in a wide array of real-world situations. Here are some examples:
-
Academic Performance: If a student answers 5 questions correctly out of 25 on a test, their score is 20%. This helps evaluate their understanding of the subject matter.
-
Sales and Discounts: A store offering a 20% discount on an item means that you'll pay 80% of the original price. Understanding percentages allows you to quickly calculate the discounted price.
-
Financial Calculations: Interest rates, tax calculations, and investment returns are all expressed as percentages. Understanding percentages is essential for making informed financial decisions.
-
Statistical Analysis: Percentages are frequently used to represent data in graphs and charts, making it easier to understand trends and patterns. For example, understanding that 20% of survey respondents prefer a certain product gives valuable market research insights.
-
Everyday Life: Calculating tips in restaurants, determining the percentage of ingredients in a recipe, or understanding sales tax are everyday instances where percentage calculations prove useful.
Beyond 5 out of 25: Generalizing Percentage Calculations
The principles discussed above apply to any fraction you want to convert to a percentage. The general formula is:
(Numerator ÷ Denominator) × 100 = Percentage
Let's consider a few more examples:
- 10 out of 50: (10 ÷ 50) × 100 = 20%
- 15 out of 75: (15 ÷ 75) × 100 = 20%
- 2 out of 10: (2 ÷ 10) × 100 = 20%
Notice that all these examples, although different in their initial fractions, all result in 20%. This demonstrates the importance of simplifying fractions before calculating the percentage; it makes the calculation more efficient and easier to understand.
Dealing with More Complex Scenarios: Decimals and Larger Numbers
The methods described above can be applied to more complex scenarios involving decimals or larger numbers. For example, calculating 12.5 out of 50 as a percentage:
(12.5 ÷ 50) × 100 = 25%
Similarly, calculating 75 out of 300 as a percentage:
(75 ÷ 300) × 100 = 25%
These examples demonstrate the versatility and broad applicability of the percentage calculation methods. Regardless of the size of the numbers, the fundamental principle remains the same: divide the numerator by the denominator and multiply the result by 100.
Frequently Asked Questions (FAQ)
Q1: What if the denominator is zero?
A1: You cannot divide by zero. A fraction with a zero denominator is undefined. In real-world terms, this means that you cannot express a portion of something if the total is zero.
Q2: How do I calculate a percentage increase or decrease?
A2: To calculate a percentage increase or decrease, find the difference between the new value and the original value, divide this difference by the original value, and then multiply by 100.
Q3: Can I use a calculator for percentage calculations?
A3: Absolutely! Calculators can greatly simplify percentage calculations, especially with more complex numbers. Most calculators have a percentage function (%) that directly calculates percentages.
Q4: Why are percentages so important?
A4: Percentages provide a standardized way to compare different quantities. They make it easier to understand proportions and make comparisons, regardless of the scale of the quantities being compared.
Conclusion: Mastering Percentages for Everyday Success
Understanding percentages is an essential life skill that extends far beyond the classroom. The ability to accurately calculate and interpret percentages is crucial for academic success, informed financial decisions, and navigating everyday situations. Through understanding the fundamental concepts of fractions, decimals, and the different methods for calculating percentages, you've gained a valuable tool for understanding and interpreting data, making sound judgments, and confidently tackling numerical challenges in various contexts. Remember the core principle: divide the part by the whole and multiply by 100 to express it as a percentage. Practice these methods, and you’ll master percentages and confidently apply them in your daily life.
Latest Posts
Latest Posts
-
4 5 X 1 6
Sep 16, 2025
-
Absolute Value Of 4 2
Sep 16, 2025
-
5 2 As A Percentage
Sep 16, 2025
-
Gcf Of 14 And 56
Sep 16, 2025
-
Lcm Of 3 4 8
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 5 Out Of 25 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.