Equivalent Fraction To 5 6
saludintensiva
Sep 10, 2025 · 5 min read
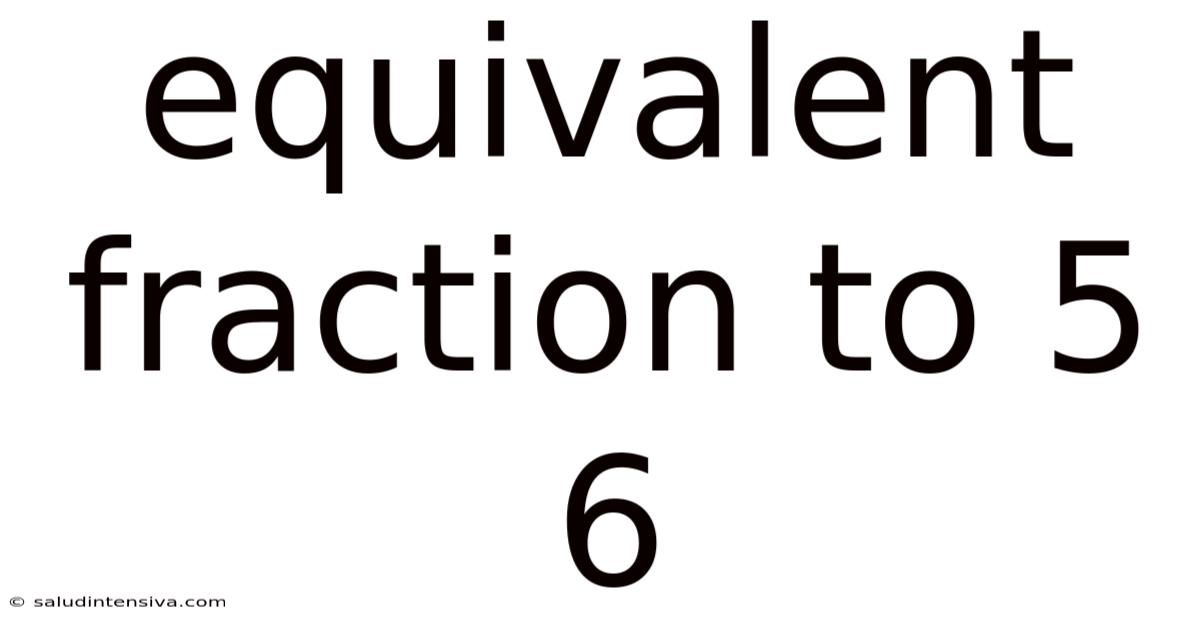
Table of Contents
Unveiling the World of Equivalent Fractions: A Deep Dive into 5/6
Finding equivalent fractions can seem daunting at first, but understanding the underlying principles transforms it into a fascinating exploration of mathematical relationships. This comprehensive guide will delve into the concept of equivalent fractions, focusing specifically on finding equivalent fractions for 5/6. We'll explore various methods, provide numerous examples, and even touch upon the practical applications of this fundamental mathematical skill. By the end, you'll not only be able to find equivalent fractions for 5/6 but also possess a solid understanding of the broader concept.
Understanding Equivalent Fractions
Before diving into the specifics of 5/6, let's establish a strong foundation. Equivalent fractions represent the same portion of a whole, even though they appear different. Think of slicing a pizza: one half (1/2) is equivalent to two quarters (2/4), or four eighths (4/8). They all represent exactly half of the pizza. The key to understanding equivalent fractions lies in the concept of multiplying or dividing both the numerator (the top number) and the denominator (the bottom number) by the same non-zero number. This process maintains the ratio and therefore the value of the fraction.
Methods for Finding Equivalent Fractions of 5/6
Several methods exist for determining equivalent fractions to 5/6. Let's explore each, providing clear examples:
1. Multiplying the Numerator and Denominator by the Same Number:
This is the most straightforward method. Choose any whole number (except zero) and multiply both the numerator (5) and the denominator (6) by that number.
-
Example 1: Multiply by 2: (5 x 2) / (6 x 2) = 10/12. Therefore, 10/12 is an equivalent fraction to 5/6.
-
Example 2: Multiply by 3: (5 x 3) / (6 x 3) = 15/18. Thus, 15/18 is another equivalent fraction.
-
Example 3: Multiply by 4: (5 x 4) / (6 x 4) = 20/24. And so on...
You can continue this process indefinitely, generating an infinite number of equivalent fractions for 5/6. Each resulting fraction represents the same portion of the whole.
2. Dividing the Numerator and Denominator by the Same Number (Simplification):
While the previous method creates larger equivalent fractions, this one aims to find smaller equivalent fractions, often leading to the simplest form of the fraction. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both numbers without leaving a remainder.
In the case of 5/6, the GCD of 5 and 6 is 1. Since 5 and 6 are relatively prime (they share no common factors other than 1), 5/6 is already in its simplest form. We cannot simplify it further.
3. Using Visual Representations:
Visual aids can greatly enhance understanding. Imagine a rectangle divided into six equal parts. Shade five of these parts to represent 5/6. Now, imagine dividing each of those six parts into two smaller equal parts. You'll now have twelve smaller parts, and ten of them will be shaded (10/12). This visually demonstrates the equivalence of 5/6 and 10/12. You can repeat this process by dividing into three, four, or more smaller parts, generating more equivalent fractions.
Exploring Equivalent Fractions Beyond the Basics
While the above methods provide the fundamental approach, let's delve into some more advanced considerations:
-
Infinite Possibilities: Remember, there are infinitely many equivalent fractions for any given fraction. We can generate as many as we need by consistently multiplying the numerator and denominator by the same number.
-
Simplest Form: Finding the simplest form of a fraction is crucial for clarity and ease of calculation. It's the equivalent fraction with the smallest whole numbers in the numerator and denominator. As noted, 5/6 is already in its simplest form.
-
Applications in Real-World Scenarios: Understanding equivalent fractions is crucial in various real-world situations, including:
- Cooking: Adjusting recipes to serve more or fewer people requires converting fractions.
- Construction: Accurate measurements in building and carpentry rely heavily on fractional calculations.
- Data Analysis: Representing data in different proportions often involves simplifying or expanding fractions.
- Sewing/Tailoring: Calculating fabric amounts and creating patterns.
Common Misconceptions about Equivalent Fractions
-
Adding or Subtracting to Numerator and Denominator: A common mistake is adding or subtracting the same number to both the numerator and denominator. This does not produce an equivalent fraction. Only multiplication or division by the same number preserves the fraction's value.
-
Incorrect GCD Calculation: Finding the greatest common divisor is critical for simplification. An incorrect GCD will lead to an incorrectly simplified fraction.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 5/6?
A1: 5/6 is already in its simplest form because 5 and 6 share no common factors other than 1.
Q2: How many equivalent fractions does 5/6 have?
A2: 5/6 has infinitely many equivalent fractions.
Q3: Is 15/18 equivalent to 5/6?
A3: Yes, 15/18 is equivalent to 5/6 because 15/18 simplifies to 5/6 (dividing both by 3).
Q4: How can I quickly check if two fractions are equivalent?
A4: Cross-multiply the numerators and denominators. If the products are equal, the fractions are equivalent. For example, for 5/6 and 10/12: (5 x 12) = 60 and (6 x 10) = 60. Since the products are equal, they are equivalent fractions.
Q5: Why is it important to learn about equivalent fractions?
A5: Understanding equivalent fractions is fundamental for various mathematical operations, including addition and subtraction of fractions, simplifying expressions, and solving real-world problems.
Conclusion
Mastering the concept of equivalent fractions is a cornerstone of mathematical proficiency. While seemingly simple, a deep understanding unlocks a powerful tool applicable across numerous fields. This guide has explored the various methods for finding equivalent fractions, focusing specifically on 5/6, and addressed common misconceptions. Remember, the key lies in consistently multiplying or dividing both the numerator and denominator by the same non-zero number. By practicing these methods and applying them to different scenarios, you’ll build confidence and enhance your overall mathematical abilities. The seemingly simple fraction 5/6 serves as a perfect springboard to understanding a vast and interconnected mathematical world.
Latest Posts
Latest Posts
-
Lcm Of 16 And 6
Sep 10, 2025
-
6 8 Divided By 2
Sep 10, 2025
-
Lcm Of 6 10 15
Sep 10, 2025
-
Centigrade To Degrees Celsius Converter
Sep 10, 2025
-
What Does 1 4 Equal
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Equivalent Fraction To 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.