Lcm Of 12 And 27
saludintensiva
Sep 18, 2025 · 5 min read
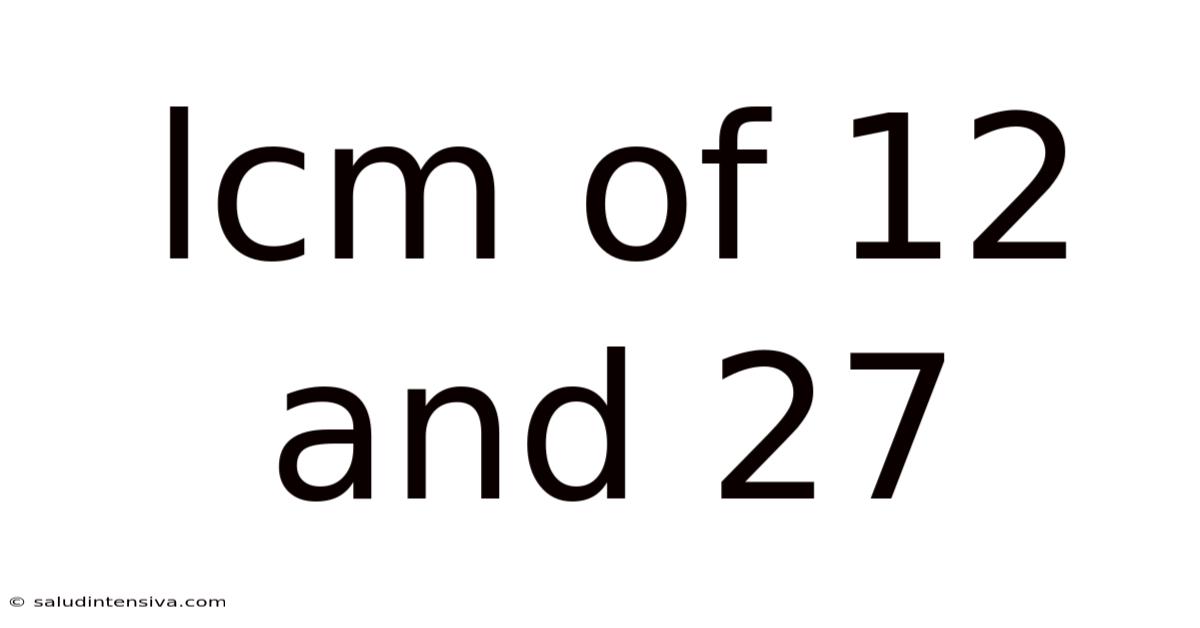
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 27: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers, like 12 and 27, might seem like a simple arithmetic task. However, understanding the underlying concepts and exploring different methods to solve this problem provides a deeper understanding of number theory and its applications. This guide will delve into the intricacies of calculating the LCM of 12 and 27, explaining various techniques and highlighting their significance in mathematics and beyond. We'll move from basic methods to more advanced strategies, ensuring a comprehensive understanding for learners of all levels.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's define what the Least Common Multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers as factors. For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21...
The common multiples are 6, 12, 18... The smallest of these common multiples is 6, making 6 the LCM of 2 and 3.
Method 1: Listing Multiples
This is the most straightforward approach, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
- Multiples of 27: 27, 54, 81, 108, 135...
By comparing the lists, we see that the smallest common multiple is 108. Therefore, the LCM of 12 and 27 is 108. While simple for small numbers, this method becomes cumbersome and inefficient for larger numbers.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3¹
- Prime factorization of 27: 3 x 3 x 3 = 3³
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(12, 27) = 2² x 3³ = 4 x 27 = 108
Method 3: Greatest Common Divisor (GCD) Method
This method uses the relationship between the LCM and the Greatest Common Divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The formula connecting LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 12 and 27 using the Euclidean algorithm:
- Divide the larger number (27) by the smaller number (12): 27 = 12 x 2 + 3
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (3): 12 = 3 x 4 + 0
- The GCD is the last non-zero remainder, which is 3.
Now, we can use the formula:
LCM(12, 27) = (12 x 27) / GCD(12, 27) = (12 x 27) / 3 = 324 / 3 = 108
Method 4: Venn Diagram Method (Visual Representation)
This method offers a visual approach to understanding the LCM concept, especially helpful for beginners. We represent the prime factorization of each number in a Venn diagram.
-
Find the prime factorization of each number:
- 12 = 2 x 2 x 3
- 27 = 3 x 3 x 3
-
Draw two overlapping circles, one for each number. Place the common prime factors (in this case, only 3) in the overlapping section. Place the unique prime factors in the non-overlapping sections.
-
The LCM is found by multiplying all the prime factors in the diagram: 2 x 2 x 3 x 3 x 3 = 108
This visual method reinforces the understanding of how the prime factors contribute to the LCM.
Applications of LCM
The concept of LCM has wide-ranging applications in various fields:
-
Scheduling: Imagine two buses leave a station at different intervals. The LCM helps determine when both buses will leave the station simultaneously again.
-
Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculations.
-
Music: The LCM is used in music theory to find the least common multiple of the lengths of musical phrases or rhythms, allowing for seamless transitions and harmonious compositions.
-
Cyclic Processes: In engineering or physics, dealing with repetitive cycles (like the rotation of gears or the oscillation of pendulums), the LCM helps determine when these cycles will coincide.
-
Computer Science: LCM finds applications in algorithms related to synchronization and scheduling of processes in computer systems.
Frequently Asked Questions (FAQ)
Q: What if I have more than two numbers? How do I find their LCM?
A: You can extend any of the methods described above to accommodate more than two numbers. For prime factorization, you consider all the prime factors from all the numbers and take the highest power of each. For the GCD method, you can find the GCD of two numbers first and then find the GCD of the result and the third number, and so on.
Q: Is there a single "best" method for finding the LCM?
A: The best method depends on the numbers involved and your comfort level with different techniques. For smaller numbers, listing multiples is easy. For larger numbers, prime factorization or the GCD method is more efficient.
Q: Why is the LCM important in mathematics?
A: The LCM is a fundamental concept in number theory, crucial for understanding divisibility, fractions, and other mathematical relationships. It forms the basis for solving many practical problems across different disciplines.
Q: Can I use a calculator to find the LCM?
A: Yes, many scientific calculators and online calculators have built-in functions to calculate the LCM of numbers.
Conclusion
Finding the LCM of 12 and 27, as we've seen, isn't just about arriving at the answer (108). It's about understanding the fundamental concepts of divisibility, prime factorization, and the relationship between LCM and GCD. The various methods presented provide different perspectives on this core mathematical idea, equipping you with the tools to tackle similar problems efficiently and confidently. Whether you prefer a visual approach, a methodical algorithmic solution, or a shortcut using the GCD, the understanding gained will serve as a solid foundation for more advanced mathematical explorations. Remember, the journey of understanding mathematical concepts is as crucial as the result itself.
Latest Posts
Latest Posts
-
3 5 Is Equivalent To
Sep 18, 2025
-
1 24 As A Percentage
Sep 18, 2025
-
Time Zone Converter Excel Formula
Sep 18, 2025
-
29 6 As A Decimal
Sep 18, 2025
-
8 25 As A Mixed Number
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.