What Is 1 4 Squared
saludintensiva
Sep 15, 2025 · 5 min read
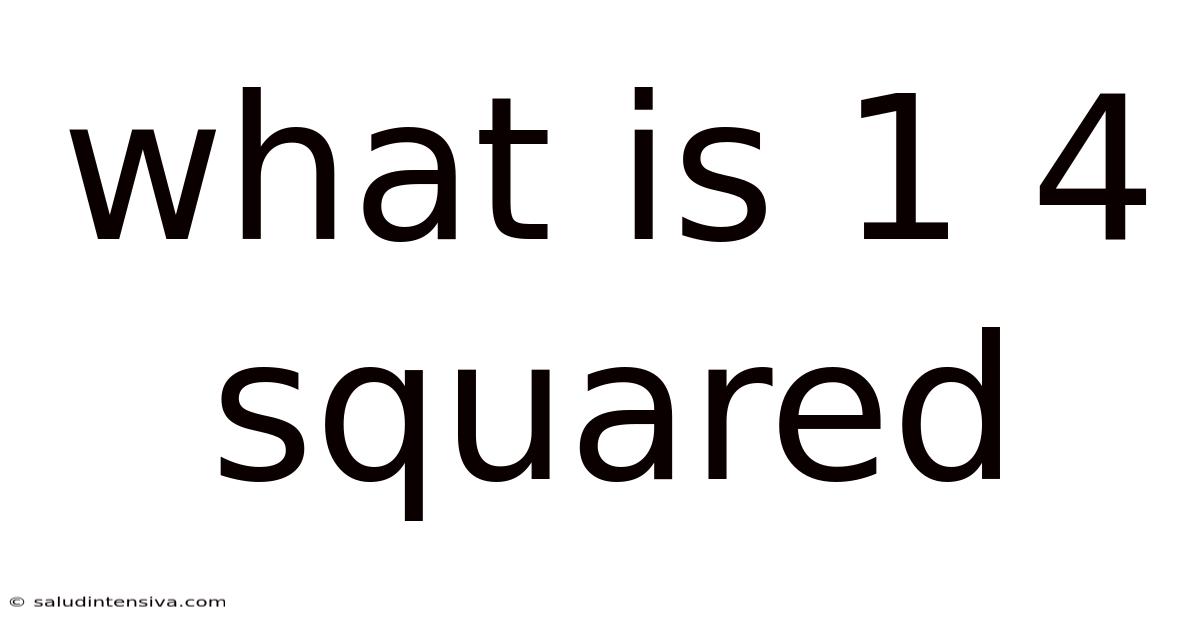
Table of Contents
Decoding 1/4 Squared: A Comprehensive Guide to Fractional Exponents
What is 1/4 squared? This seemingly simple question opens a door to a deeper understanding of exponents, fractions, and their interplay. This comprehensive guide will not only answer that question directly but also explore the underlying mathematical principles, providing a solid foundation for anyone wanting to master these concepts. We'll cover various approaches, delve into the scientific notation, and address frequently asked questions to solidify your comprehension.
Understanding Exponents and Fractions
Before diving into 1/4 squared, let's refresh our understanding of exponents and fractions. An exponent (or power) indicates how many times a base number is multiplied by itself. For instance, 2³ (2 cubed) means 2 x 2 x 2 = 8. The number 3 is the exponent, and 2 is the base.
Fractions, on the other hand, represent parts of a whole. 1/4 (one-fourth) signifies one part out of four equal parts. Understanding both concepts is crucial for tackling fractional exponents.
Calculating 1/4 Squared: The Direct Approach
The question "What is 1/4 squared?" translates mathematically to (1/4)². This means we need to multiply 1/4 by itself:
(1/4)² = (1/4) x (1/4)
To multiply fractions, we multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(1 x 1) / (4 x 4) = 1/16
Therefore, 1/4 squared is 1/16.
Alternative Methods: Expanding the Understanding
While the direct method is straightforward, exploring other approaches deepens our understanding of exponents and fractions.
Method 1: Converting to Decimal
We can convert the fraction 1/4 to its decimal equivalent (0.25) before squaring:
(1/4)² = (0.25)² = 0.25 x 0.25 = 0.0625
This decimal, 0.0625, is equivalent to 1/16. This method demonstrates the interchangeability between fractions and decimals in mathematical operations.
Method 2: Applying the Power to Both Numerator and Denominator
Another approach involves applying the exponent to both the numerator and the denominator separately:
(1/4)² = (1²) / (4²) = 1/16
This method highlights the distributive property of exponents over fractions. It's a particularly useful technique when dealing with more complex fractional exponents.
Visualizing 1/4 Squared: A Geometric Approach
Visualizing mathematical concepts can be incredibly helpful. Imagine a square with sides of length 1 unit. Dividing this square into four equal smaller squares creates four parts, each representing 1/4 of the original square. If we now take one of these smaller squares (1/4) and create a smaller square from it with sides of 1/4, the area of this smaller square would be (1/4) x (1/4) = 1/16 of the original square. This visual representation perfectly illustrates the result of 1/4 squared.
Exploring Higher Powers of 1/4
Let's extend our understanding by calculating higher powers of 1/4:
- (1/4)³ = (1/4) x (1/4) x (1/4) = 1/64
- (1/4)⁴ = (1/4) x (1/4) x (1/4) x (1/4) = 1/256
- (1/4)^n = 1/4^n
Notice the pattern: As the exponent increases, the denominator (the bottom number) becomes a higher power of 4, while the numerator remains 1. This pattern holds true for any positive integer exponent.
Negative Exponents and 1/4
What happens when the exponent is negative? A negative exponent signifies the reciprocal of the base raised to the positive exponent. For example:
(1/4)^-1 = 4¹ = 4 (1/4)^-2 = (4¹)² = 16 (1/4)^-n = 4^n
This means that a negative exponent reverses the fraction.
Scientific Notation and 1/4 Squared
Scientific notation is a way of expressing numbers, especially very large or very small numbers, in a concise and standardized form. While not strictly necessary for 1/4 squared, understanding scientific notation is beneficial for working with more complex calculations. 1/16 in scientific notation is 6.25 x 10⁻².
Real-World Applications of Fractional Exponents
Fractional exponents are not just abstract mathematical concepts; they have numerous practical applications in various fields:
- Physics: Calculating decay rates in radioactive materials.
- Engineering: Determining the stress and strain on materials under pressure.
- Finance: Calculating compound interest over time.
- Computer Science: Modeling algorithms and data structures.
Understanding fractional exponents is essential for anyone working in these and related fields.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve (1/4)²?
A: Yes, most calculators can handle fractional exponents. You can either enter it directly as (1/4)^2 or as 0.25^2.
Q: What if the numerator of the fraction is not 1?
A: The same principles apply. For example, (3/4)² = (3/4) x (3/4) = 9/16. You can apply the exponent to both the numerator and the denominator or convert to decimals before squaring.
Q: How do I handle more complex fractional exponents like (1/4)^2.5?
A: This involves understanding fractional exponents further. (1/4)^2.5 can be rewritten as (1/4)^(5/2). This is equivalent to the square root of (1/4) raised to the power of 5, or (√(1/4))^5 = (1/2)^5 = 1/32. This requires a deeper understanding of root functions and their relationship to fractional exponents.
Q: Are there any online resources to help me practice?
A: Yes, many online educational websites and apps offer practice problems and tutorials on exponents and fractions. Search for "exponents practice problems" or "fractional exponents calculator" to find suitable resources.
Conclusion
Understanding what 1/4 squared equals—namely, 1/16—is only the starting point. This comprehensive guide has explored various methods of calculating fractional exponents, emphasizing the importance of grasping both the procedural and conceptual aspects. By understanding the underlying principles of exponents and fractions, you're equipped to tackle more complex mathematical challenges and apply these concepts to real-world problems. Remember, practice is key to mastering these fundamental concepts. Continue exploring, experiment with different approaches, and don't hesitate to seek additional resources to solidify your understanding. With consistent effort, you'll build a strong foundation in mathematics, opening doors to further learning and exploration.
Latest Posts
Latest Posts
-
1 5 Divided By 4
Sep 15, 2025
-
Find Halfway Between Two Locations
Sep 15, 2025
-
5 2 5 As A Decimal
Sep 15, 2025
-
3 1 10 As A Decimal
Sep 15, 2025
-
5 2 6 2 5 6
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 4 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.