1.6 As A Mixed Number
saludintensiva
Sep 17, 2025 · 5 min read
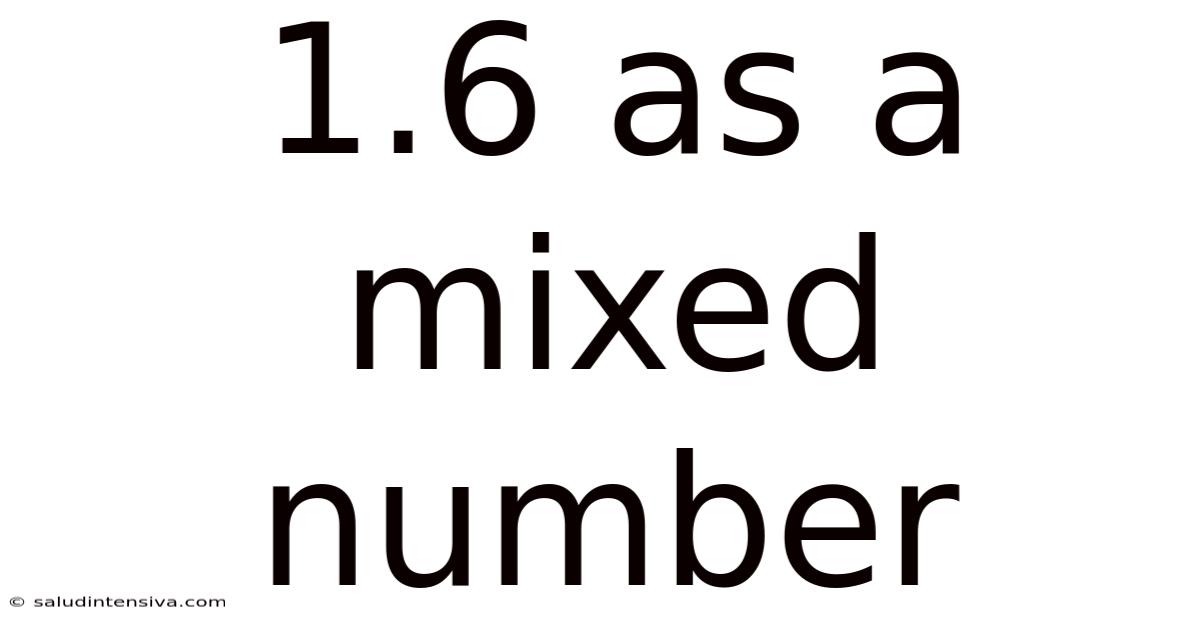
Table of Contents
Understanding 1.6 as a Mixed Number: A Comprehensive Guide
The decimal number 1.6 might seem simple at first glance, but understanding its representation as a mixed number reveals a deeper understanding of fractions and decimal relationships. This comprehensive guide will explore the conversion process, delve into the underlying mathematical principles, and address common questions surrounding this seemingly straightforward concept. We'll break down the process step-by-step, ensuring you grasp not just the answer but also the why behind it. This knowledge is crucial for various mathematical applications, from basic arithmetic to more advanced algebraic concepts.
Understanding Decimals and Mixed Numbers
Before we jump into converting 1.6, let's clarify the definitions.
-
Decimals: Decimals represent fractions where the denominator is a power of 10 (10, 100, 1000, etc.). The digits to the right of the decimal point represent the numerator, while the place value of each digit indicates the denominator. For instance, 1.6 means 1 + 6/10.
-
Mixed Numbers: A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). For example, 1 ¾ is a mixed number, representing one whole unit and three-quarters of another.
Our goal is to represent the decimal 1.6 as a mixed number, effectively combining a whole number with a fractional part.
Converting 1.6 to a Mixed Number: A Step-by-Step Approach
The conversion process is relatively straightforward. Here's how to transform 1.6 into its mixed number equivalent:
Step 1: Identify the Whole Number Part
The digit to the left of the decimal point represents the whole number part. In 1.6, the whole number is clearly 1.
Step 2: Convert the Decimal Part to a Fraction
The digits to the right of the decimal point represent the fractional part. In 1.6, this is 0.6. To convert this decimal to a fraction, we write it as a fraction with a denominator of 10 (since there's one digit after the decimal point):
0.6 = 6/10
Step 3: Simplify the Fraction (If Possible)
Always simplify your fractions to their lowest terms. Both 6 and 10 are divisible by 2:
6/10 = 3/5
Step 4: Combine the Whole Number and the Simplified Fraction
Combine the whole number from Step 1 and the simplified fraction from Step 3 to form the mixed number:
1 + 3/5 = 1 3/5
Therefore, 1.6 expressed as a mixed number is 1 3/5.
Illustrative Examples: Expanding the Concept
Let's solidify our understanding with a few more examples. This will help you apply the conversion process to different decimal numbers.
Example 1: Converting 2.75 to a Mixed Number
- Whole number: 2
- Decimal part: 0.75 = 75/100
- Simplify the fraction: 75/100 = 3/4 (dividing both numerator and denominator by 25)
- Mixed number: 2 + 3/4 = 2 ¾
Example 2: Converting 0.8 to a Mixed Number
- Whole number: 0
- Decimal part: 0.8 = 8/10
- Simplify the fraction: 8/10 = 4/5 (dividing both numerator and denominator by 2)
- Mixed number: 0 + 4/5 = 4/5 (Note: Since the whole number is 0, the result is simply a proper fraction.)
Example 3: Converting 3.125 to a Mixed Number
- Whole number: 3
- Decimal part: 0.125 = 125/1000
- Simplify the fraction: 125/1000 = 1/8 (dividing both numerator and denominator by 125)
- Mixed number: 3 + 1/8 = 3 ⅛
These examples showcase the versatility of the conversion method. Regardless of the number of decimal places, the fundamental steps remain the same.
The Mathematical Rationale: Connecting Fractions and Decimals
The conversion from a decimal to a mixed number hinges on the fundamental relationship between fractions and decimals. Decimals are essentially a specific type of fraction where the denominator is a power of 10. By expressing the decimal part as a fraction and then simplifying, we're simply representing the same value in a different format. The whole number part remains unchanged throughout the conversion process because it represents the integer component of the original decimal value.
Frequently Asked Questions (FAQ)
Q1: Can all decimals be expressed as mixed numbers?
A1: Not all decimals can be expressed as mixed numbers. Decimals that are whole numbers (e.g., 3.0, 10.0) will simply be whole numbers when converted. Decimals that are less than 1 (e.g., 0.75) will result in proper fractions. However, all decimals can be represented as either a whole number, a proper fraction, or a mixed number.
Q2: What if the fraction doesn't simplify?
A2: If the fraction resulting from the conversion of the decimal part cannot be simplified further (meaning the greatest common divisor of the numerator and denominator is 1), you leave the fraction as it is. For instance, if you had 1.37 and converted it to 1 and 37/100, you wouldn't simplify it further because 37 and 100 share no common factors greater than 1.
Q3: Is there a quicker method for converting certain decimals?
A3: While the step-by-step method is comprehensive and universally applicable, some decimals can be converted more intuitively. For example, you might recognize that 0.5 is equivalent to ½, 0.25 is equivalent to ¼, and 0.75 is equivalent to ¾. This knowledge can expedite the conversion process for common decimal fractions.
Q4: Why is understanding this conversion important?
A4: Mastering the conversion between decimals and mixed numbers is fundamental for a strong grasp of mathematical concepts. It strengthens your understanding of fractions, builds your ability to work with different number representations, and provides a foundational skill for more advanced mathematical concepts in algebra, geometry, and calculus.
Conclusion: Mastering the Conversion and Beyond
Converting 1.6 to the mixed number 1 3/5 might seem like a small step, but it exemplifies a significant mathematical principle: the interchangeable nature of fractions and decimals. Through a step-by-step approach, we've not only learned how to perform this specific conversion but also built a deeper understanding of the relationship between these two fundamental number representations. This knowledge will serve as a solid base for tackling more complex mathematical problems in the future. The ability to move fluidly between decimals and fractions is a crucial skill for anyone pursuing mathematical studies or applying mathematical concepts in various fields. Remember to practice these conversions regularly to solidify your understanding and increase your confidence in handling various numerical problems.
Latest Posts
Latest Posts
-
3 1 As A Percentage
Sep 17, 2025
-
27 2 As A Mixed Number
Sep 17, 2025
-
Whats 20 Percent Of 13
Sep 17, 2025
-
Is 1 2 Greater Than 2 3
Sep 17, 2025
-
16 20 As A Percent
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1.6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.